Exercícios para o ENEM (197)

(Enem 2021) Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = ± A cos (ωt) ou P(t) = ± A sen (ωt), em que A ＞ 0 é a amplitude de deslocamento máximo e ω é a frequência, que se relaciona com o período T pela fórmula ω = 2π/T.

Considere a ausência de quaisquer forças dissipativas.

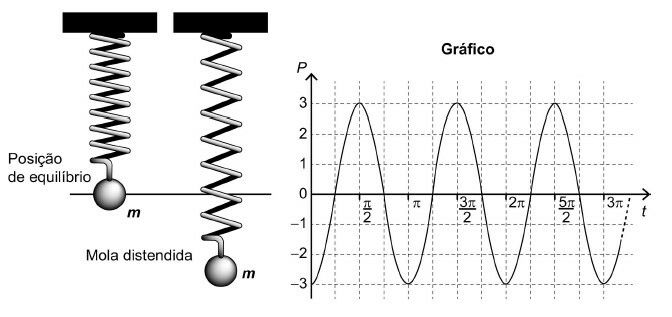
A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é

(Enem 2018) Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:

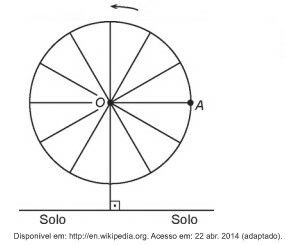
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t.

Após duas voltas completas, f em o seguinte gráfico:

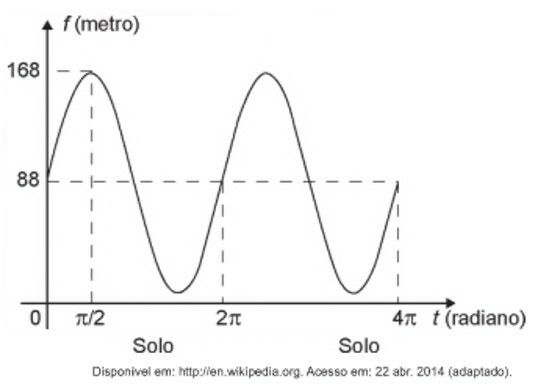
A expressão da função altura é dada por

(CEDERJ 2014) O valor máximo da função real é:

(UECE 2021) No plano, com o sistema de coordenadas cartesianas usual, a interseção dos gráficos das funções reais de variável real f(x)=sen(x) e g(x)=cos(x) são, para cada número inteiro k, os pontos P(xk, yk). Então, os possíveis valores para yk são

A inclinação da reta que passa pelos pontos A (0,2) e B (2,0) é

Calcule o valor de t, sabendo que os pontos A (0, 1), B (3, t) e C (2, 1) são colineares.

Os coeficientes, angular e linear, da reta x - y + 2 = 0 são, respectivamente,

Obtenha a equação da reta que possui o gráfico a seguir.

Determine a equação da reta r que passa pelo ponto A(3, 1) e que tem coeficiente angular m = -2 .

Encontre as coordenadas do ponto de intersecção entre a reta r: x + y - 3 = 0 e a reta que passa pelos pontos A(2, 3) e B(1, 2).