Exercícios para o ENEM (12)
Foram encontradas 2456 questões
Dona Maria, diarista na casa da família Teixeira, precisa fazer café...
Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
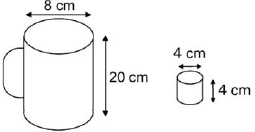
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
Um satélite de telecomunicações, t minutos após ter atingido sua...
Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por
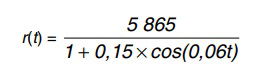
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
12 765 km.
12 000 km.
11 730 km.
10 965 km.
5 865 km.
Uma empresa vende tanques de combustíveis de formato cilíndrico, em...
Uma empresa vende tanques de combustíveis de formato cilíndrico, em três tamanhos, com medidas indicadas nas figuras. O preço do tanque é diretamente proporcional à medida da área da superfície lateral do tanque. O dono de um posto de combustível deseja encomendar um tanque com menor custo por metro cúbico de capacidade de armazenamento.
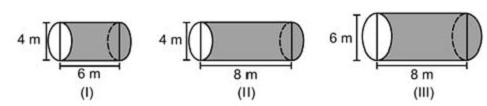
Qual dos tanques deverá ser escolhido pelo dono do posto? (Considere π ≅ 3)
I, pela relação área/capacidade de armazenamento de 1⁄3
I, pela relação área/capacidade de armazenamento de 4⁄3
II, pela relação área/capacidade de armazenamento de 3⁄4
III, pela relação área/capacidade de armazenamento de 2⁄3
III, pela relação área/capacidade de armazenamento de 7⁄12
A figura a seguir é a representação de uma região por meio de...
A figura a seguir é a representação de uma região por meio de curvas de nível, que são curvas fechadas representando a altitude da região, com relação ao nível do mar. As coordenadas estão expressas em graus de acordo com a longitude, no eixo horizontal, e a latitude, no eixo vertical. A escala em tons de cinza desenhada à direita está associada à altitude da região.
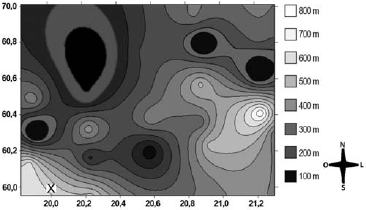
Um pequeno helicóptero usado para reconhecimento sobrevoa a região a partir do ponto X = (20; 60). O helicóptero segue o percurso:
Ao final, desce verticalmente até pousar no solo.
De acordo com as orientações, o helicóptero pousou em um local cuja altitude é
menor ou igual a 200 m.
maior que 200 m e menor ou igual a 400 m.
maior que 400 m e menor ou igual a 600 m.
maior que 600 m e menor ou igual a 800 m.
maior que 800 m.
Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado,...
Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Recíproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e a altura, uma variável de dimensões lineares. As fórmulas que determinam esses índices são:

Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m2 , então ela possui RIP igual a
0,4 cm/kg1/3 .
2,5 cm/kg1/3 .
8 cm/kg1/3 .
20 cm/kg1/3 .
40 cm/kg1/3 .
Um balão atmosférico, lançado em Bauru (34 quilômetros a Noroeste...
Um balão atmosférico, lançado em Bauru (34 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de mediação.
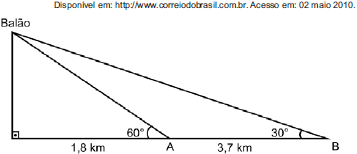
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.
Qual a altura aproximada em que se encontrava o balão?
1,8 km
1,9 km
3,1 km
3,7 km
5,5 km
Em canteiros de obras de construção civil é comum perceber...
Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
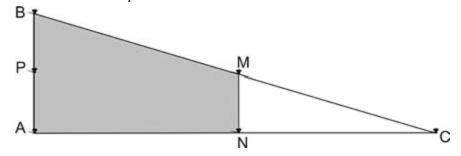
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde
à mesma área do triângulo AMC.
à mesma área do triângulo BNC.
à metade da área formada pelo triângulo ABC.
ao dobro da área do triângulo MNC.
ao triplo da área do triângulo MNC.
Nos processos industriais, como na indústria de cerâmica, é...
Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função
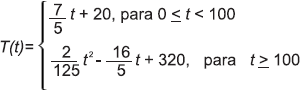
em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 °C e retirada quando a temperatura for 200 °C.
O tempo de permanência dessa peça no forno é, em minutos, igual a
100.
108.
128.
130.
150.
Marco e Paulo foram classificados em um concurso. Para classificação...
Marco e Paulo foram classificados em um concurso. Para classificação no concurso o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio padrão dos dois candidatos.
Dados dos candidatos no concurso

O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é
Marco, pois a média e a mediana são iguais.
Marco, pois obteve menor desvio padrão.
Paulo, pois obteve a maior pontuação da tabela, 19 em Português.
Paulo, pois obteve maior mediana.
Paulo, pois obteve maior desvio padrão.
Ronaldo é um garoto que adora brincar com números. Numa dessas...
Ronaldo é um garoto que adora brincar com números. Numa dessas brincadeiras, empilhou caixas numeradas de acordo com a sequência conforme mostrada no esquema a seguir.
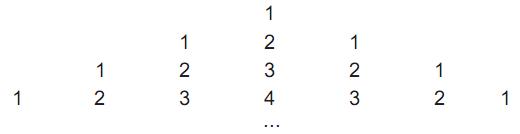
Ele percebeu que a soma dos números em cada linha tinha uma propriedade e que, por meio dessa propriedade, era possível prever a soma de qualquer linha posterior às já construídas.
A partir dessa propriedade, qual será a soma da 9ª linha da sequência de caixas empilhadas por Ronaldo?
9
45
64
81
285
