Exercícios sobre potência mecânica e rendimento
A potência mecânica e o rendimento são conceitos fundamentais para compreender como máquinas, motores e sistemas de transporte realizam trabalho e transformam energia. Neste conjunto de exercícios no estilo ENEM, você poderá aplicar fórmulas, interpretar situações reais e avaliar o desempenho de diferentes dispositivos — de guindastes a bicicletas elétricas. Resolva as questões, confira o gabarito comentado e aprimore sua habilidade de analisar problemas que envolvem força, trabalho e eficiência.
Questão 1
Em um canteiro de obras, um guindaste elétrico é utilizado para erguer verticalmente uma carga de concreto de 500 kg a uma altura de 20 metros. A operação de içamento é realizada em 10 segundos com velocidade constante. O motor do guindaste, no entanto, não é perfeito e possui um rendimento de 80%, o que significa que parte da energia elétrica que ele consome é perdida na forma de calor e som.
Considerando a aceleração da gravidade como g = 10 m/s2, qual é a potência elétrica total consumida pelo motor do guindaste para realizar essa tarefa?
a) 8,0 kW
b) 10,0 kW
c) 12,5 kW
d) 50,0 kW
Resposta correta: alternativa c) 12,5 kW
Esta questão exige o cálculo da potência útil (a potência efetivamente usada para levantar a carga) e, em seguida, o uso do rendimento para encontrar a potência total (a potência que o motor realmente consome da rede elétrica).
Primeiro vamos calcular o trabalho útil ou Wútil. Ele é a energia necessária para vencer a força peso da carga ao longo da altura de içamento.
Wútil = força × distância = peso x distância
Wútil = (m . g) . h
Wútil = (500 . 10) . 20 = 5000 . 20 = 100.000 J
Agora calculamos a potência útil ou Pútil . Lembre que a potência útil considera a rapidez com que o trabalho útil é realizado, ou seja, o trabalho dividido pelo tempo.
Vamos agora determinar a potência total consumida ou Ptotal. O rendimento (η) é a razão entre a potência útil e a potência total consumida, ou:
O rendimento é de 80% = 80 / 100 = 0,8. A potência total é:
Portanto, a potência elétrica total consumida pelo motor do guindaste é 12,5 kW.
Questão 2
Para garantir o abastecimento de água em uma propriedade rural, foi instalado um sistema de bombeamento que eleva a água de um poço até um reservatório localizado 15 metros acima do nível da água no poço. O motor da bomba precisa elevar um volume de 3.000 litros de água em 5 minutos para encher o reservatório. Sabe-se que o sistema motor-bomba possui um rendimento total de 75%.
Considere a densidade da água como 1 kg/L e a aceleração da gravidade como g=10 m/s2.
A potência elétrica, em quilowatts (kW), que o motor da bomba consome da rede elétrica para realizar essa tarefa é de:
a) 1,5 kW
b) 2,0 kW
c) 2,5 kW
d) 1,125 kW
Resposta correta: alternativa b) 2,0 kW
Esta questão envolve calcular a potência necessária para elevar a massa de água (potência útil) e, em seguida, usar o rendimento para descobrir a potência real que o motor consome (potência total).
O primeiro passo é calcular a massa de água que será elevada. O enunciado trouxe que a densidade da água é 1 kg/L, e que são elevados 3.000 litros de água. A densidade é definida como: d = m / V. Então:
mágua = V . d = 3000 . 1 = 3000 kg
Vamos agora calcular o trabalho útil ou Wútil. Lembre que o trabalho útil é a energia gasta para elevar a massa de água contra a gravidade e corresponde à variação da energia potencial gravitacional.
A energia potencial gravitacional é dada por Epot = m . g . h
Wútil = m . g . h
Wútil = 3000 . 10 . 15 = 450000 J
Tendo o trabalho útil podemos calcular a potência útil ou Pútil, isso porque a potência é o trabalho realizado por unidade de tempo. Lembre que é necessário converter o tempo para segundos.
Δt = 5 minutos = 5 . 60 = 300 s
Tendo o rendimento da bomba e a potência útil podemos calcular a potência total consumida Ptotal. Lembre que 75% = 75 / 100 = 0,75, e que o rendimento (η) relaciona a potência útil com a potência total. Temos então:
Portanto, a potência elétrica total consumida pelo motor da bomba é de 2 kW.
Questão 3
Uma bicicleta elétrica tornou-se uma opção de transporte sustentável em muitas cidades. Um ciclista, cuja massa somada à da bicicleta é de 90 kg, utiliza o motor elétrico para auxiliá-lo a subir uma longa rampa com velocidade constante de 18 km/h. A inclinação da rampa é tal que, para cada 10 metros percorridos, o ciclista sobe 1 metro na vertical. O motor da bicicleta opera com um rendimento de 80% e as forças de atrito e resistência do ar somadas resultam em uma força constante de 30 N, contrária ao movimento.
Considerando a aceleração da gravidade como g=10 m/s2, qual é a potência elétrica que o motor precisa consumir da bateria para manter a subida nessas condições?
a) 450 W
b) 600 W
c) 750 W
d) 900 W
Resposta correta: alternativa c) 750 W
Para resolver esta questão, precisamos primeiro determinar a potência mecânica útil necessária para mover a bicicleta e, depois, usar o rendimento para encontrar a potência elétrica total consumida.
O primeiro passo é escrever todas as unidades no Sistema Internacional (SI). A velocidade precisa estar em metros por segundo (m/s). Temos:
Vamos agora calcular as forças que o motor precisa vencer. Como a velocidade é constante, a força resultante deve ser igual a zero. Assim, a força exercida pelo motor ou Fmotor deve ser igual à soma das forças resistivas do ar e do atrito. O enunciado trouxe que a força resistiva FR total é de 30 N.
Observe o esquema das forças atuantes sobre a bicicleta:
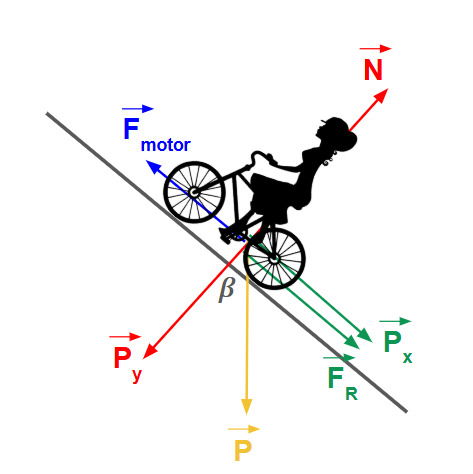
Temos que:
O módulo da força peso ou P é:
P = m.g = 90 . 10 = 900 N
Para determinar o valor de Px que é a projeção do peso no eixo x paralelo ao plano inclinado, vamos usar a seguinte informação do enunciado: "a cada 10 m percorridos sobe-se 1 m". Temos então a seguinte relação:
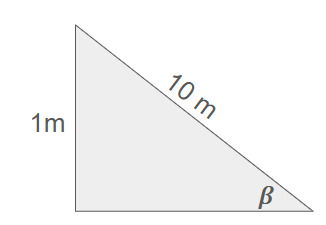
A inclinação do plano nos dá o seno do ângulo
Assim o valor de Px pode ser determinado:
Tendo Px e FR podemos determinar a força do motor Fmotor:
Fmotor = Px + FR = 90 + 30 = 120 N
Vamos agora calcular a potência útil ou Pútil. Lembre que a potência útil é a potência mecânica que efetivamente move a bicicleta, e pode ser determinada multiplicando a força pela velocidade:
Pútil = Fmotor . v
Pútil = 120 . 5 = 600 W
Tendo a potência útil, usamos o rendimento para determinar a potência total. O rendimento (η) de 80% equivale a 0,8, pois 80% = 80 / 100 = 0,8
A potência elétrica que o motor consome da bateria é de 750 W.
Questão 4
A potência mecânica é um conceito fundamental na física para descrever a rapidez com que um motor ou uma força pode realizar trabalho, sendo crucial para a análise de desempenho de veículos, máquinas e até mesmo de atletas. No contexto automotivo, a potência do motor está diretamente ligada à capacidade do carro de acelerar e de manter velocidades elevadas, especialmente ao enfrentar resistências como o arrasto do ar e a inclinação de uma rampa.
Com base nos princípios da dinâmica e da energia, analise as seguintes afirmações sobre potência mecânica:
I. Um motor é considerado mais potente que outro não por ser capaz de realizar um trabalho maior, mas por ser capaz de realizar o mesmo trabalho em um intervalo de tempo menor.
II. Para um veículo se deslocar com velocidade constante em uma estrada horizontal, a potência mecânica útil desenvolvida pelo seu motor é nula, pois a força resultante sobre o veículo é zero.
III. Suponha que um motor de carro elétrico possa entregar uma potência mecânica constante em uma certa faixa de operação. Ao encontrar uma subida íngreme, o motor terá que exercer uma força maior para vencer a componente da força peso. Consequentemente, para manter a potência constante, a velocidade do veículo necessariamente diminuirá.
Classifique as afirmações como verdadeiras (V) ou falsas (F) e marque a alternativa correta.
a) F, V, F
b) V, V, F
c) F, F, V
d) V, F, V
Resposta correta: alternativa d) V, F, V
Vamos analisar cada uma das afirmações:
I. Um motor é considerado mais potente que outro não por ser capaz de realizar um trabalho maior, mas por ser capaz de realizar o mesmo trabalho em um intervalo de tempo menor.
Esta afirmação descreve perfeitamente a definição de potência. A potência (P) é a taxa de realização de trabalho (W) no tempo, ou seja, P = W / Δt. Se dois motores realizam o mesmo trabalho (W), aquele que o fizer em menor tempo (Δt) terá a maior potência.
Conclusão: A afirmação é Verdadeira (V).
II. Para um veículo se deslocar com velocidade constante em uma estrada horizontal, a potência mecânica útil desenvolvida pelo seu motor é nula, pois a força resultante sobre o veículo é zero.
A Primeira Lei de Newton diz que, para um veículo em velocidade constante, a força resultante é nula. Isso significa que o módulo da força motriz exercida pelo motor (Fmotor) é igual, em módulo, à soma de todas as forças resistivas ou FR resultantes da resistência do ar, do atrito dos pneus, etc.
No entanto, a potência mecânica útil do motor é calculada como Pútil = Fmotor . v . Como nem a força do motor (Fmotor) nem a velocidade (v) são nulas, a potência desenvolvida pelo motor para vencer as resistências também não é nula. O erro está em confundir força resultante nula com força motriz nula.
Conclusão: A afirmação é Falsa (F).
III. Suponha que um motor de carro elétrico possa entregar uma potência mecânica constante [...]. Ao encontrar uma subida íngreme, o motor terá que exercer uma força maior [...]. Consequentemente, para manter a potência constante, a velocidade do veículo necessariamente diminuirá.
A potência mecânica instantânea é dada por P = F . v, onde F é a força na direção do movimento e v é a velocidade. Se a potência (P) é mantida constante, a força e a velocidade são inversamente proporcionais (v = P / F). Ao subir uma ladeira, o motor precisa aplicar uma força (F) maior para vencer não só as resistências habituais, mas também a componente da força peso que se opõe ao movimento, chamada de Px. Se F aumenta e P é constante, a velocidade (v) deve, obrigatoriamente, diminuir. Isso descreve exatamente por que os carros perdem velocidade em subidas se o motorista não aumentar a potência fornecida (pisando mais no acelerador).
Conclusão: A afirmação é Verdadeira (V).
A sequência correta é V, F, V.
Questão 5
O rendimento mecânico é um parâmetro crucial na engenharia para avaliar a eficiência de qualquer máquina que converte energia de uma forma para outra, como um motor elétrico que converte energia elétrica em trabalho mecânico. Na prática, nenhuma máquina é perfeita, e parte da energia total que ela consome (Ptotal) é inevitavelmente perdida, principalmente devido ao atrito e à resistência do ar, sendo transformada em calor. A energia que efetivamente realiza a tarefa desejada é chamada de energia útil (Pútil). O rendimento (η) é a razão entre essas duas energias.
Considerando o motor de uma escada rolante em um shopping center, analise as seguintes afirmações sobre seu rendimento mecânico:
I. Se o motor da escada rolante possui um rendimento de 75%, isso significa que 75% da potência elétrica total consumida por ele é convertida em potência mecânica útil (para mover os degraus e os passageiros), enquanto os 25% restantes são dissipados, principalmente na forma de calor devido ao atrito interno e perdas elétricas.
II. Ao operar vazia, sem passageiros, a escada rolante atinge seu rendimento mecânico máximo, pois o motor realiza o menor esforço possível, consumindo apenas a energia para mover sua própria estrutura.
III. Para realizar um mesmo trabalho útil (por exemplo, elevar uma certa massa de passageiros a uma determinada altura), um sistema com maior rendimento mecânico necessariamente consumirá uma menor quantidade de energia total da fonte elétrica.
Classifique as afirmações como verdadeiras (V) ou falsas (F) e marque a alternativa correta:
a) V, V, F
b) F, V, V
c) V, F, V
d) F, F, V
Resposta correta: alternativa c) V, F, V
Vamos analisar cada uma das afirmações:
I. Se o motor da escada rolante possui um rendimento de 75%, isso significa que 75% da potência elétrica total consumida por ele é convertida em potência mecânica útil [...], enquanto os 25% restantes são dissipados [...].
Esta afirmação descreve exatamente a definição de rendimento. O rendimento (η) é a fração da potência total (Ptotal) que é convertida em potência útil (Pútil). O restante, 1−η, corresponde à potência dissipada (Pdissipada). Se η=0,75 (ou 75%), então 75% da energia é útil e 25% é dissipada.
Conclusão: A afirmação é Verdadeira (V).
II. Ao operar vazia, sem passageiros, a escada rolante atinge seu rendimento mecânico máximo, pois o motor realiza o menor esforço possível [...].
Esta afirmação é um erro conceitual comum. O rendimento é η = Pútil / Ptotal. A "potência útil" de uma escada rolante é a potência usada para elevar os passageiros. Quando ela opera vazia, não há passageiros sendo elevados, portanto, a potência útil é zero (Pútil). No entanto, o motor ainda consome uma potência total (Ptotal) para vencer o atrito interno e mover a massa dos próprios degraus. Como o numerador é zero e o denominador é diferente de zero, o rendimento nessas condições é, na verdade, 0%.
Conclusão: A afirmação é Falsa (F).
III. Para realizar um mesmo trabalho útil [...], um sistema com maior rendimento mecânico necessariamente consumirá uma menor quantidade de energia total [...].
A relação é η=Pútil / Ptotal, que pode ser reescrita como Ptotal = Pútil / η. Se a potência útil (Pútil) for a mesma em duas situações (mesma tarefa), o sistema com maior rendimento (η) terá um denominador maior, resultando em uma menor potência total (Ptotal) consumida. Isso significa que máquinas mais eficientes são mais econômicas energeticamente para realizar a mesma tarefa.
Conclusão: A afirmação é Verdadeira (V).
A sequência correta é V, F, V.
Questão 6
O desempenho de um carro elétrico moderno depende diretamente da capacidade de seu motor em converter energia elétrica da bateria em trabalho mecânico para movimentar o veículo. A potência do motor determina a aceleração e a velocidade máxima, enquanto seu rendimento indica quão eficientemente essa conversão de energia ocorre, impactando diretamente a autonomia do veículo.
Com base nos conceitos de potência mecânica e rendimento, analise as seguintes afirmações a respeito do funcionamento de um carro elétrico:
I. A potência mecânica útil, que efetivamente impulsiona o carro vencendo as forças de resistência (atrito e arrasto do ar), é sempre menor que a potência elétrica total drenada da bateria, devido a perdas inevitáveis por efeito Joule no motor e atrito em componentes mecânicos.
II. O torque máximo do motor de um carro elétrico (que se traduz na força máxima de tração) ocorre em baixas rotações. Portanto, a potência mecânica máxima do veículo também é desenvolvida quando ele está partindo do repouso ou se movendo muito lentamente.
III. Se dois carros elétricos idênticos, com motores de mesma potência total, sobem a mesma rampa com a mesma velocidade constante, mas o motor do carro A possui um rendimento de 90% e o do carro B possui 80%, isso significa que o motor do carro A está operando com uma "folga" de potência maior que o do carro B.
Classifique as afirmações como verdadeiras (V) ou falsas (F) e marque a alternativa correta.
a) V, F, F
b) V, F, V
c) F, V, V
d) V, V, F
Resposta correta: alternativa b) V, F, V
Vamos analisar cada uma das afirmações:
I. A potência mecânica útil [...] é sempre menor que a potência elétrica total drenada da bateria, devido a perdas inevitáveis [...].
Esta afirmação descreve a essência do rendimento mecânico. A potência total (Ptotal) é a energia que o motor consome da bateria por segundo. A potência útil (Pútil) é a parte dessa energia que efetivamente se torna movimento. A diferença entre elas é a potência dissipada (Pdissipada), perdida principalmente como calor. Como nenhuma máquina real tem rendimento de 100% (η<1), a potência útil será sempre uma fração da potência total (Pútil = η . Ptotal), sendo, portanto, menor.
Conclusão: A afirmação é Verdadeira (V).
II. O torque máximo [...] ocorre em baixas rotações. Portanto, a potência mecânica máxima [...] também é desenvolvida quando ele está partindo do repouso [...].
É verdade que motores elétricos entregam torque máximo (força de rotação) em rotações muito baixas, ou até mesmo nulas. Contudo, a potência mecânica é o produto da força pela velocidade (P = F . v). Ao partir do repouso, a velocidade (v) é zero. Portanto, a potência naquele instante também é zero, apesar da força ser máxima. A potência máxima é atingida em uma velocidade intermediária, onde o produto de força (que já começou a diminuir) e velocidade é o maior possível.
Conclusão: A afirmação é Falsa (F).
III. Se dois carros [...] sobem a mesma rampa com a mesma velocidade constante, mas o motor do carro A possui um rendimento de 90% e o do carro B possui 80%, [...] o motor do carro A está operando com uma "folga" de potência maior [...].
Se os carros são idênticos e sobem a mesma rampa com a mesma velocidade, a tarefa mecânica é a mesma para ambos. Isso significa que a potência útil (Pútil) necessária é a mesma para os dois. Vamos calcular a potência total que cada um precisa consumir para gerar essa Pútil:
Carro A: Ptotal, A = Pútil / 0,90 ≈ 1,11 . Pútil
Carro B: Ptotal, B = Pútil / 0,80 = 1,25 Pútil
O motor do carro B precisa consumir mais energia da bateria para realizar a mesma tarefa. Como ambos os motores têm a mesma potência total máxima de fábrica, o motor B está operando mais próximo de seu limite de consumo. Consequentemente, o motor A, por ser mais eficiente, realiza a tarefa com mais facilidade, consumindo menos de sua capacidade total, o que significa que ele tem uma "folga" de potência maior.
Conclusão: A afirmação é Verdadeira (V).
A sequência correta é V, F, V.
Questão 7
Em uma oficina mecânica, um guincho elétrico é utilizado para levantar um bloco de motor de 200 kg do chão até uma altura de 3 metros. A operação é realizada em 5 segundos, com o guincho consumindo uma potência elétrica constante de 1500 W da rede elétrica durante o processo.
Considere a aceleração da gravidade como g=10 m/s2. Com base nesses dados, analise as seguintes afirmações:
I. O rendimento mecânico do motor do guincho nesta operação é de 80%.
II. A potência dissipada na forma de calor e som pelo motor é de 400 W.
III. Se fosse necessário erguer o mesmo bloco de motor com o dobro da velocidade, a potência útil desenvolvida pelo motor também dobraria, mas o rendimento da máquina permaneceria inalterado.
Classifique as afirmações como verdadeiras (V) ou falsas (F) e marque a alternativa correta.
a) V, F, F
b) V, V, F
c) F, V, V
d) V, F, V
Resposta correta: alternativa a) V, F, F
Para classificar as afirmações, primeiro vamos calcular os valores de trabalho útil e potência útil da operação.
Cálculo do trabalho útil. Lembre que ele dá a energia gasta para vencer a força peso do motor.
Wútil = Força Peso . Altura = (m . g) . h
Wútil = (200 .10) . 3 m = 6000 J
A potência útil ou Pútil mede a taxa com que o trabalho útil é realizado.
Pútil = Wútil / Δt = 6000 / 5 = 1200 W
Agora, vamos analisar cada afirmação.
I. O rendimento mecânico do motor do guincho nesta operação é de 80%.
O rendimento (η) é a razão entre a potência útil e a potência total consumida.
η = Pútil / Ptotal = 1200 / 1500 = 0,8
Um rendimento de 0,8 corresponde a 80%.
Conclusão: A afirmação é Verdadeira (V).
II. A potência dissipada na forma de calor e som pelo motor é de 400 W.
A potência dissipada (Pdissipada) é a diferença entre a potência total consumida e a potência útil.
Pdissipada = Ptotal − Pútil = 1500 − 1200 = 300 W
A afirmação diz que a potência dissipada é de 400 W, o que é incorreto.
Conclusão: A afirmação é Falsa (F).
III. Se fosse necessário erguer o mesmo bloco de motor com o dobro da velocidade, a potência útil desenvolvida pelo motor também dobraria, mas o rendimento da máquina permaneceria inalterado.
Esta afirmação tem duas partes.
Primeira parte: A potência útil é dada por Pútil = F . v. Como a força para levantar o bloco (Força Peso) é constante, se dobrarmos a velocidade (v), a potência útil (Pútil) também dobrará. Esta parte está correta.
Segunda parte: Afirma que o rendimento permaneceria inalterado. O rendimento de uma máquina não é necessariamente constante e pode variar com a carga e a velocidade de operação. Geralmente, operar um motor muito acima ou muito abaixo de sua condição ideal pode diminuir seu rendimento. Portanto, não se pode garantir que o rendimento seria o mesmo. A afirmação assume uma constância que não é garantida na física real de um motor.
Conclusão: A afirmação é Falsa (F), pois não podemos assumir que o rendimento se manterá constante sob condições de operação diferentes.
A sequência correta é V, F, F.
Continue praticando com exercícios de Física para 1º ano do Ensino Médio.
Exercícios sobre potência mecânica e rendimento. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-potencia-mecanica-e-rendimento/. Acesso em:

