Transformações cíclicas da termodinâmica

Uma transformação cíclica ou um ciclo termodinâmico é uma sequência de processos termodinâmicos que faz com que um sistema retorne ao seu estado inicial após uma série de mudanças. Isso significa que, ao final do ciclo, todas as variáveis de estado do sistema (pressão, volume, temperatura, energia interna etc.) voltam aos seus valores originais.

Imagine um balão de ar. Se você o esquenta, ele expande. Depois, você o resfria e ele se comprime, voltando ao seu tamanho e temperatura originais. Isso seria uma transformação cíclica.

O sistema balão + ar dentro do balão passa por várias etapas ao ser aquecido e resfriado, mas termina exatamente como começou.

Neste conteúdo você encontra:

• Quando ocorrem essas transformações
• Principais características e o papel da Primeira Lei da Termodinâmica
• Tipos de transformações cíclicas
  • Ciclos de máquinas térmicas (Motores)
  • Ciclos de refrigeração e bombas de calor
• Como resolver questões envolvendo Ciclos Termodinâmicos (passo a passo)
• Exemplos

Quando ocorrem essas transformações

Elas são a base do funcionamento de diversas máquinas e sistemas que operam continuamente, como por exemplo:

• Motores de combustão ou máquinas térmicas: como os motores de carros, turbinas a vapor e turbinas a gás. Nesses sistema eles convertem energia térmica em trabalho mecânico.
• Refrigeradores e bombas de calor: operam em ciclos que movem calor de uma região mais fria para uma mais quente, ou vice-versa, com o uso de trabalho externo.
• Sistemas de geração de energia: usinas termelétricas, por exemplo, que operam em ciclos para converter calor em eletricidade.

Principais características e o papel da Primeira Lei da Termodinâmica

A característica principal de uma transformação cíclica é dada pela Primeira Lei da Termodinâmica, que afirma que a variação da energia interna do sistema é igual ao calor trocado com o sistema menos o trabalho realizado pelo sistema, ou:

ΔU = Q−W

Onde:

• ΔU é a variação da energia interna do sistema;
• Q é o calor trocado com o sistema. Q > 0 se o sistema absorve ou recebe calor, e Q < 0 se o sistema cede calor;
• W é o trabalho realizado pelo sistema. W > 0 se o sistema realiza trabalho, e W < 0 se o trabalho é realizado sobre o sistema.

Agora, vamos aplicar essa lei a um ciclo:

Variação da energia interna (ΔU=0): por definição, em uma transformação cíclica, o sistema retorna ao seu estado inicial. A energia interna do sistema (U) é uma função do estado do sistema, isso significa que seu valor depende apenas do estado atual do sistema, e não do caminho percorrido para chegar lá. Como o estado inicial é igual ao estado final, a variação total da energia interna ao longo de um ciclo é sempre zero ou ΔU_ciclo= 0.

Consequência da Primeira Lei: se ΔU_ciclo=0, então a Primeira Lei traz que 0 = Q_total - W_total e Q_total = W_total para um ciclo.

Calor e trabalho não são individualmente iguais a zero: embora ΔU seja zero em um ciclo, o Q e o W não são necessariamente zero para um ciclo completo. Eles representam as trocas de energia que ocorrem ao longo das etapas do ciclo. Apenas o total ou saldo final entre eles é igual, ou seja, Q_total = W_total.

Diagramas PV ou Pressão versus Volume:

• O trabalho realizado por um sistema em uma transformação pode ser visualizado como a área sob a curva em um diagrama PV.

• Em uma transformação cíclica, o trabalho total é a área delimitada pela curva fechada no diagrama PV.

• Sentido horário: se o ciclo é percorrido no sentido horário no diagrama PV, o trabalho líquido realizado pelo sistema é positivo ou W_total> 0. Isso caracteriza uma máquina térmica que produz trabalho.

• Sentido anti-horário: se o ciclo é percorrido no sentido anti-horário no diagrama PV, o trabalho líquido realizado pelo sistema é negativo ou W_total < 0. Isso significa que trabalho foi realizado sobre o sistema (ou seja, o sistema consumiu trabalho) para que o ciclo ocorresse. Isso caracteriza um refrigerador ou uma bomba de calor.

Tipos de transformações cíclicas

Podemos classificar as transformações cíclicas com base na sua finalidade:

Ciclos de máquinas térmicas (Motores)

Objetivo: Converter calor em trabalho mecânico.

Característica: Absorvem calor de uma fonte quente, liberam parte desse calor para uma fonte fria e utilizam a diferença para realizar trabalho.

Sentido no PV: Horário.

Eficiência (η): Mede quão bem o ciclo converte calor em trabalho.

Como o W_total = Q_absorvido - Q_cedido, podemos escrever o rendimento como sendo:

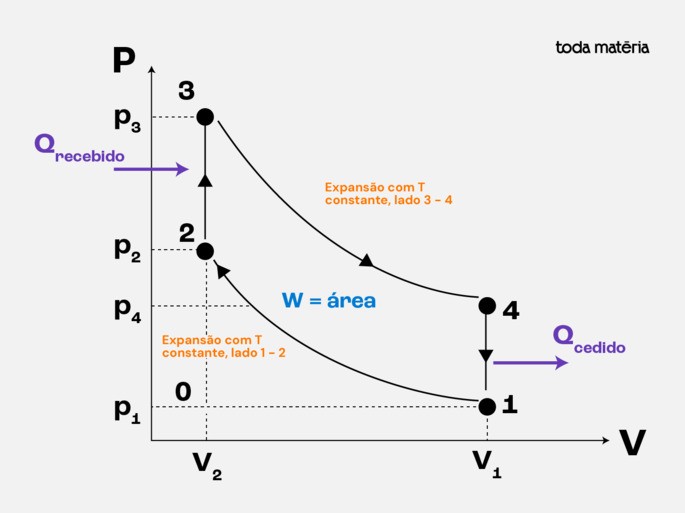
Ciclo de Carnot (ideal)

É o ciclo mais eficiente possível que pode operar entre duas temperaturas, T_Q (quente) e T_F (fria). É composto por duas transformações isotérmicas e duas adiabáticas.

• Importância: serve como um limite teórico para a eficiência de qualquer máquina térmica. Nenhuma máquina real pode ser mais eficiente que uma máquina de Carnot operando entre as mesmas temperaturas.
• Eficiência de Carnot: η_Carnot= 1 − T_F / T_Q . Onde as temperaturas são dadas em Kelvin!
• Não é prático: devido à necessidade de transformações isotérmicas e adiabáticas perfeitas e reversíveis, não pode ser implementado na prática.

Abaixo mostramos o diagrama do Ciclo de Carnot:

Aprofunde os seus estudos sobre o ciclo de Carnot.

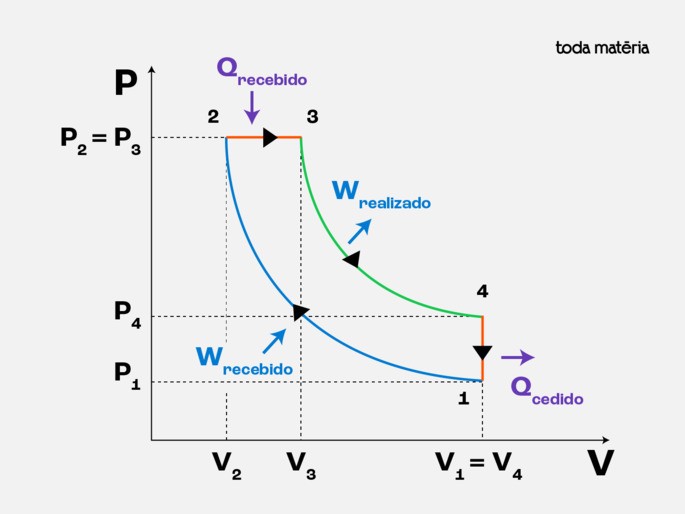
Ciclo Otto (motor a gasolina)

• Descrição: composto por duas transformações adiabáticas (compressão e expansão) e duas transformações isocóricas (volume constante - absorção e rejeição de calor).
• Aplicação: motores de automóveis movidos a gasolina.

Abaixo mostramos o diagrama do Ciclo OTTO:

Ciclo Diesel (motor a diesel)

• Descrição: similar ao Otto, mas a absorção de calor ocorre a pressão constante (isobárica) em vez de volume constante.
• Aplicação: motores de automóveis, caminhões e embarcações movidos a diesel.

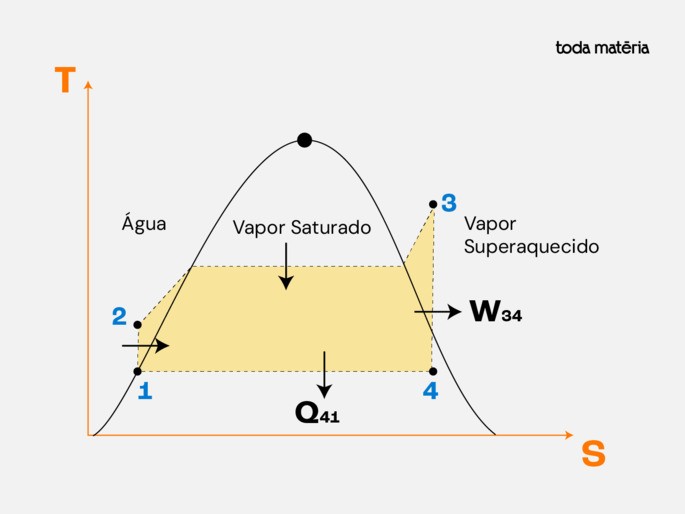
Ciclo Rankike (usinas a vapor)

• Descrição: utiliza água como fluido de trabalho, passando pelas fases líquida e gasosa. Composto por bombeamento (líquido), aquecimento na caldeira (evaporação), expansão na turbina (vapor) e condensação.
• Aplicação: geração de eletricidade em usinas termelétricas.

Abaixo mostramos o diagrama Temperatura (T) versus Entropia (S) do Ciclo Rankine:

Ciclos de refrigeração e bombas de calor

Mover calor de uma região mais fria para uma mais quente, ou de uma região mais quente para uma ainda mais quente. Isso exige um trabalho externo sobre o sistema, pois o calor não se desloca na direção esperada.

Característica: invertem o fluxo natural do calor.

Sentido no PV: anti-horário.

Coeficiente de Desempenho (COP): mede a eficiência desses ciclos, mas não é uma porcentagem como a eficiência, podendo ser maior que 1.

Ciclo de Carnot inverso (ideal)

O inverso do ciclo de Carnot, onde o trabalho é fornecido ao sistema para mover calor.

Importância: Define o limite teórico para o desempenho de refrigeradores e bombas de calor.

COP de Refrigerador:

COP de Bomba de Calor:

Note que COP_bomba= COP_refrig+1

Abaixo mostramos o diagrama Temperatura (T) versus Entropia (S) do Ciclo de Carnot Inverso:

Ciclo de refrigeração por compressão de vapor

É o ciclo mais comum em refrigeradores domésticos e sistemas de ar condicionado. Envolve a evaporação de um fluido refrigerante a baixa pressão e temperatura (absorvendo calor do ambiente frio), compressão do vapor, condensação a alta pressão e temperatura (liberando calor para o ambiente quente) e expansão.

Aplicação: geladeiras, freezers, ar condicionado.

Abaixo mostramos o diagrama Temperatura (T) versus Entropia (S) do Ciclo de Refrigeração por Compressão de Vapor:

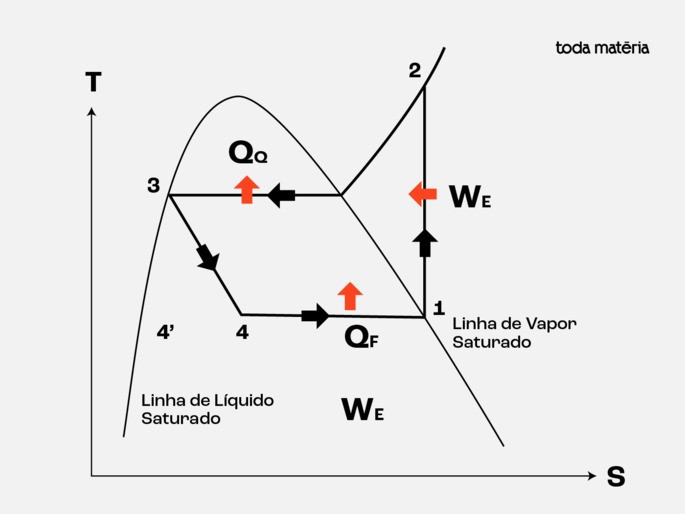
Ciclo de bomba de calor

Essencialmente o mesmo hardware de um refrigerador, mas a finalidade é transferir calor de um ambiente externo (frio) para um ambiente interno (quente) para aquecimento.

Aplicação: Aquecimento de ambientes em climas frios.

Como resolver questões envolvendo Ciclos Termodinâmicos (passo a passo)

1. Desenhe ou analise o Diagrama PV

• Trabalho: A área dentro do ciclo representa o trabalho total ou ∣W_total∣.
• Sentido: Se a direção do processo for no sentido horário o trabalho total será positivo ou W_total > 0 e o sistema é de um máquina térmica. Se for anti-horário, W_total < 0 e o sistema será o de um refrigerador ou bomba de calor.
• Lembre-se: trabalho positivo é realizado pelo sistema durante uma expansão, trabalho negativo é feito sobre o sistema em uma compressão.

2. Aplique a Primeira Lei da Termodinâmica

• Lembre que para qualquer ciclo temos ΔU_ciclo = 0.
• Consequentemente, Q_total = W_total. Este é o seu ponto de partida para a maioria dos cálculos.

3. Identifique Q_absorvido e Q_cedido

• Q_total é a soma algébrica de todo o calor trocado. E é dado pela diferença entre o calore recebido e cedido, ou: Q_absorvido − Q_cedido, considerando Q_cedido como positivo.
• Analise cada etapa do ciclo: onde o calor é absorvido (geralmente em processos de aquecimento ou expansão isotérmica) e onde é cedido (geralmente em processos de resfriamento ou compressão isotérmica).

4. Use as fórmulas de eficiência ou de COP

• Máquina Térmica:
• Refrigerador:
• Bomba de Calor:
• Use as temperaturas em Kelvin nas fórmulas de eficiência e de COP.

5. Atenção aos sinais das grandezas

• Calor (Q): Positivo se absorvido pelo sistema, e negativo se cedido pelo sistema.
• Trabalho (W): Positivo se realizado pelo sistema (expansão), negativo se realizado sobre o sistema (compressão).
• É comum usar o módulo do trabalho ou |W_total| quando se fala em "trabalho consumido" ou "trabalho necessário".

6. Decomponha o ciclo

Se o problema não fornecer os valores totais, você pode precisar calcular Q e W para cada etapa individual (isobárica, isocórica, isotérmica e adiabática) e depois somá-los para encontrar Q_total e W_total.

Exemplos

Considere um mol (1 mol) de um gás ideal que passa por um ciclo termodinâmico composto por quatro etapas, conforme ilustrado no diagrama PV abaixo:

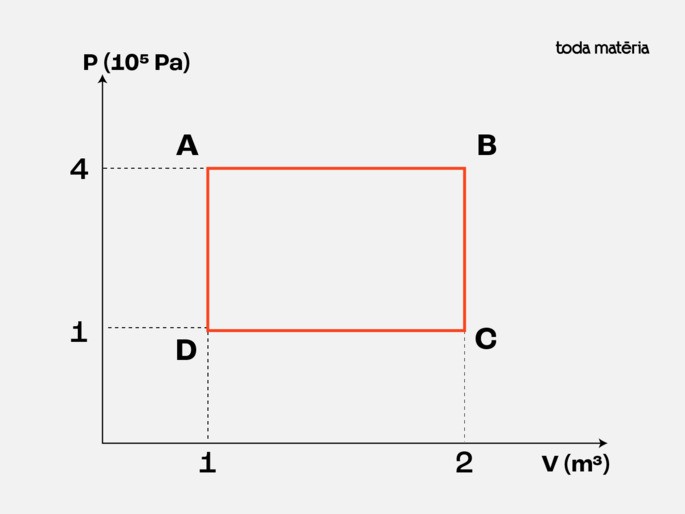
Dados:

• Número de mols (n) = 1 mol
• Constante dos gases ideais (R) = 8,314 J / (mol.K)
• Assume-se um gás monoatômico ideal, que possui Calor Específico Molar a Volume Constante igual a

Pede-se:

1. Calcule a temperatura em cada ponto do ciclo.
2. Calcule o trabalho (W), o calor (Q) e a variação da energia interna (ΔU) para cada processo.
3. Calcule o trabalho total (W_total), o calor total (Q_total) e a variação total da energia interna (ΔU_ciclo) para o ciclo completo.
4. Determine a eficiência térmica do ciclo.

Resolução:

1. Vamos primeiro determinar a temperatura em cada ponto do ciclo lembrando que: PV = n.R.T. Isolando T temos:

Ponto	P (105 Pa)	V (m3)	R	T (K)
A	4	1	8,314	48112
B	4	2	8,314	96223
C	1	2	8,314	24056
D	1	1	8,314	12028

2. Vamos agora calcular o trabalho (W), o calor (Q) e a variação da energia interna (ΔU) para cada processo. Para tanto, lembre-se que:

Processo	A ⇒ B	B ⇒ C	C ⇒ D	D ⇒ A
Tipo de processo	Expansão Isobárica	Resfriamento Isocórico	Compressão Isobárica	Aquecimento Isocórico
	4.105 - 4.105 = 0 Pa	1.105 - 4.105 = - 3.105 Pa	1.105 - 1.105 = 0 Pa	4.105 - 1.105 = 3.105 Pa
	2 - 1 = 1 m3	2 - 2 = 0 m3	1 - 2 = - 1 m3	1 - 1 = 0 m3
	96223 - 48112 = 48111 K	24056 - 96223 = - 72167 K	12028 - 24056 = - 12028 K	48112 - 12028 = 36084 K
	(4.105).1 = 4.105 J	0 J, pois o volume é constante	1 . 105 . (-1) = - 1. 105 J	0 J, pois o volume é constante
	1.1,5.8,314.48111 = 6.105 J	1.1,5.8,314.(-72167) = - 9.105 J	1.1,5.8,314.(-12028) = - 1,5.105 J	1.1,5.8,314.36084 = 4,5.105 J
	6.105 + 4.105 = 10.105 J	(- 9.105) + 0 = - 9.105 J	(-1,5.105) + (-1.105) = - 2,5.105 J	4,5.105 + 0 = 4,5 . 105 J

3. Vamos agora fazer os cálculos para o ciclo completo.

Lembre que nesse caso Q_ciclo é a soma de todos os Q, W_ciclo é a soma de todos os W e ΔU_ciclo é a soma de todos os ΔU. Ficamos com:

ΔU_ciclo = 6.10⁵ + (- 9.10⁵) + (-1,5.10⁵) + 4,5.10⁵ = 0.10⁵ = 0 J, confirmando que a variação da energia interna em uma transformação cíclica é igual a zero.

W_total = 4.10⁵ + 0 + (- 1.10⁵) + 0 = 3.10⁵ J.

Lembre que o trabalho total pode ser calculado tambéem pela área total dentro da curva. Podemos, então, conferir o valor calculando a área do retângulo ABCD. Lembre que a área do retângulo é igual a base vezes a altura ou:

área = (2 - 1) . (4 - 1) = 1 . 3 = 3 J

Como o valor do trabalho é positivo, temos que o sistema é uma máquina térmica, ou seja, ela gera trabalho.

Q_total = 10.10⁵ + (- 9.10⁵) + (- 2,5.10⁵) + 4,5.10⁵ = 3.10⁵ J

Observe que W_total = Qtotal, que confirma a Primeira Lei da Termodinâmica para transformações cíclicas.

4. Vamos agora determinar a eficiência do sistema ()

Lembre que a eficiência é dada pela relação entre o trabalho realizado e o calor absorvido pelo sistema, ou:

Observe pelo diagrama e pela tabela acima que o sistema absorve calor apenas em dois processos, a saber, A ⇒ B e D ⇒ A. Assim o calor absorvido é igual a 10.10⁵ J + 4,5.10⁵ J = 14,5.10⁵ J. A eficiência fica então:

ou aproximadamente 21%.

Este exemplo ilustra como aplicar a Primeira Lei da Termodinâmica em cada etapa de um ciclo e, em seguida, para o ciclo completo. Os resultados confirmam os princípios-chave das transformações cíclicas:

• A variação da energia interna para o ciclo completo é zero (ΔU_ciclo=0).
• O calor total trocado é igual ao trabalho total realizado (Q_total = W_total).
• O trabalho total é igual a área delimitada pelo ciclo no diagrama PV.
• A eficiência é a razão entre o trabalho total produzido e o calor total absorvido.

Dominar o conceito de transformações cíclicas é crucial para entender o funcionamento de vários equipamentos usados atualmente no cotidiano. Lembre-se sempre do princípio fundamental: o sistema retorna ao estado original, implicando ΔU=0 e, consequentemente, Q_total = W_total.

Para praticar: Exercícios sobre transformações cíclicas da termodinâmica (com gabarito)

Estude mais sobre:

Segunda Lei da Termodinâmica

Primeira Lei da Termodinâmica.