Simetria: tipos, definição e atividades para imprimir
Simetria é um conceito relacionado ao equilíbrio. Na matemática, pertence ao campo da geometria, que estuda como um objeto pode manter-se idêntico quando submetido a certas transformações, como reflexões, rotações ou translações.
Fora da matemática, a simetria pode ser observada na natureza, como nas asas de uma borboleta ou nas folhas de uma planta. Além disso, a arte, a arquitetura, a tecnologia e até a física utilizam conceitos geométricos de simetria.

Matematicamente, a simetria ocorre em relação aos elementos básicos da geometria: ponto, reta e plano. Um arranjo de formas (planas ou espaciais) é dito simétrico quando cada elemento pode ser transposto em relação a um ponto, reta ou plano, sem alterar suas proporções ou ângulos.
Tudo que não é simétrico é considerado assimétrico.

Tipos de Simetria
A simetria pode ser classificada quanto aos seus tipos ou, técnicas para produzir formas geométricas simétricas.
Simetria de Reflexão (ou Simetria Espelhada)
A simetria de reflexão ocorre quando uma figura é refletida, resultando idêntica à original, como em um espelho. Amplamente utilizada nas artes e arquitetura, baseia-se em um eixo ou ponto de reflexão.
Em um plano cartesiano, cada ponto de uma imagem refletida está a mesma distância de um eixo que seu ponto equivalente da imagem original.
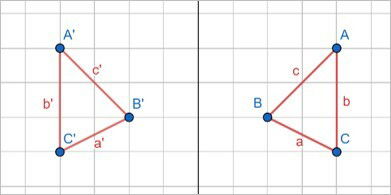
Na imagem anterior, A e A' estão a quatro unidades da reta vertical, B e B' a duas unidades e C e C' também a quatro unidades. O resultado é uma imagem refletida invertida.

Simetria de Translação
A simetria de translação refere-se à mudança de posição de um objeto sem espelhamento. Na translação, a alteração na posição do objeto mantém suas dimensões, sentido e direção, garantindo que as imagens produzidas sejam congruentes.
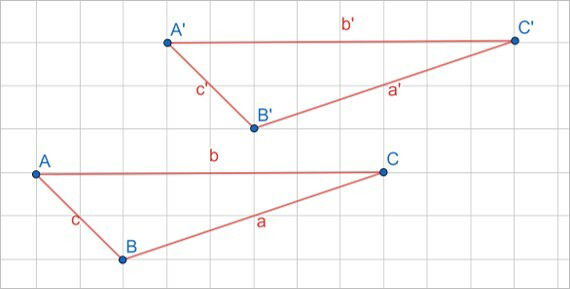
Na imagem, o triângulo ABC foi transladado para A'B'C', ou seja, ele apenas mudou de lugar, conservando suas características.
Simetria de Rotação
A simetria de rotação ocorre quando uma figura é girada em torno de um ponto, por um determinado ângulo. Imagens simétricas por rotações são congruentes, ou seja, iguais em forma e dimensões.
Nas rotações, dois parâmetros devem ser bem estabelecidos: o ponto a partir do qual o giro ocorre e o quanto a figura gira, normalmente medido em graus.
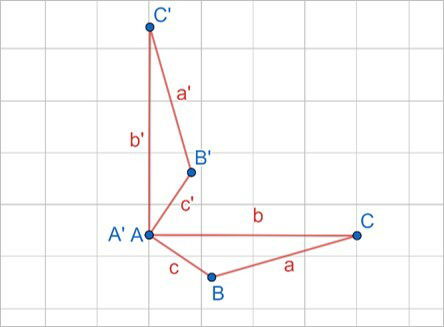
O triângulo ABC girou 90º em relação ao ponto A. Assim, A e A' estão na mesma posição.
Veja mais sobre transformações geométricas: translação, rotação e reflexão.
Simetria bilateral e radial
Simetria bilateral: ocorre quando um objeto pode ser dividido em duas partes idênticas por um único plano de simetria.

Simetria Radial: ocorre quando um objeto pode ser dividido em várias partes idênticas ao redor de um ponto central ou eixo. Esse tipo de simetria é caracterizado por múltiplos planos de simetria que passam pelo ponto ou eixo central.

A simetria dos fractais
A curva de Koch, foi uma das primeiras descobertas na teoria dos fractais. Ela foi introduzida pelo matemático sueco Helge von Koch em 1904.
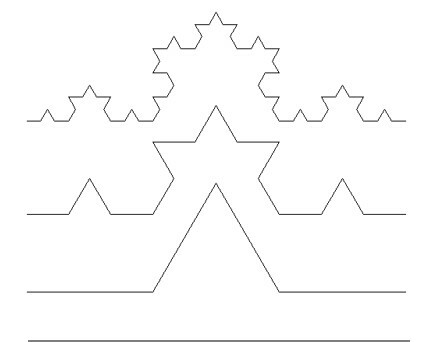
A construção da curva de Koch começa com um segmento de linha reta. Esta linha é dividida em três partes iguais e o terço do meio substituído por dois segmentos de linha que formam um ângulo, criando um pico em forma de triângulo equilátero.
Esse processo é repetido infinitamente para cada novo segmento de linha. Cada iteração adiciona mais detalhes e complexidade à curva.
Atividades de simetria para imprimir
Folha 1

Folha 2

ASTH, Rafael. Simetria: tipos, definição e atividades para imprimir. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/simetria/. Acesso em:


