Matemática no Enem 2025: os conteúdos que mais caem
A prova de matemática do Enem (Matemática e suas tecnologias) é a única prova que apresenta uma disciplina isolada, o que a torna o maior peso individual do concurso.
As questões da prova são objetivas, com 5 alternativas de resposta, apresentam enunciados contextualizados e cobram um conhecimento global do aluno.
Justamente por ser a única disciplina isolada no Enem, Matemática pode definir sua nota final — para melhor ou para pior. Com o Toda Matéria+, você estuda com foco nos assuntos que mais caem, pratica com exercícios inéditos com gabarito comentado por professores, e aprende estratégias para resolver até os enunciados mais longos com mais rapidez e segurança.
Veja os conteúdos de Matemática mais cobrados no Enem dos últimos 10 anos:
1. Grandezas proporcionais
Grandezas proporcionais, que engloba os conteúdos de razão e proporção, regra de três, porcentagem e escalas, é o que mais aparece nas questões de Matemática.
O fato deste conteúdo ser aplicado nas mais variadas situações do cotidiano, faz com que seja muito explorado no Enem.
Esse tipo de cálculo pode aparecer em questões que cobrem diretamente a relação entre grandezas ou em problemas onde este cálculo é usado em uma das etapas da sua resolução.
Questão 1
(Enem - 2017) Às 17 h 15 min começa uma forte chuva, que cai com intensidade constante. Uma piscina em forma de um paralelepípedo retângulo, que se encontrava inicialmente vazia, começa a acumular a água da chuva e, às 18 horas, o nível da água em seu interior alcança 20 cm de altura. Nesse instante, é aberto o registro que libera o escoamento da água por um ralo localizado no fundo dessa piscina, cuja vazão é constante. Às 18 h 40 min a chuva cessa e, nesse exato instante, o nível da água na piscina baixou para 15 cm.
O instante em que a água dessa piscina terminar de escoar completamente está compreendido entre
a) 19 h 30 min e 20 h 10 min
b) 19 h 20 min e 19 h 30 min
c) 19 h 10 min e 19 h 20 min
d) 19 h e 19 h 10 min
e) 18 h 40 min e 19 h
Você entendeu a lógica dessa questão? É esse tipo de raciocínio que mais aparece no Enem. Com o Toda Matéria+, você resolve exercícios inéditos com gabaritos comentados por especialistas, aprende com resumos visuais e treina com simulados por tema, tudo organizado como o Enem cobra.
Leia sobre proporção.
2. Estatística, gráficos e tabelas
Cálculo de média, moda e mediana são os conteúdos de estatística que mais aparecem na prova de Matemática. Além disso, as questões que envolvam a interpretação de gráficos (estatísticos ou não) e tabelas são muito recorrentes.
Aliás, os gráficos estão presentes não só na prova de Matemática, mas também de outras disciplinas como Física, Geografia, Biologia e Química.
Na prova de Matemática, muitas vezes, a interpretação do gráfico é apenas uma etapa da resolução da questão, sendo necessário aplicar outros conhecimentos.
Questão 2
(Enem - 2017) Dois reservatórios A e B são alimentados por bombas distintas por um período de 20 h. A quantidade de água contida em cada reservatório nesse período pode ser visualizada na figura.
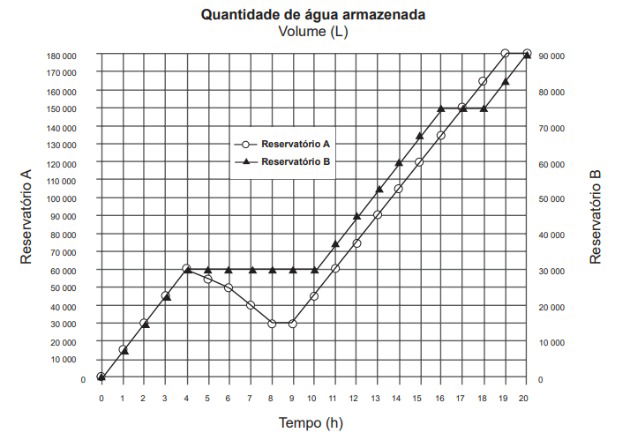
O número de horas em que os dois reservatórios contêm a mesma quantidade de água é
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
3. Aritmética
Questões com cálculos simples, que envolvam frações ou números decimais, problemas relacionados com princípio da contagem, também aparecem com frequência.
Questão 3
(Enem - 2017) Em um parque há dois mirantes de alturas distintas que são acessados por elevador panorâmico. O topo do mirante 1 é acessado pelo elevador 1, enquanto que o topo do mirante 2 é acessado pelo elevador 2. Eles encontram-se a uma distância possível de ser percorrida a pé, e entre os mirantes há um teleférico que os liga que pode ou não ser utilizado pelo visitante.
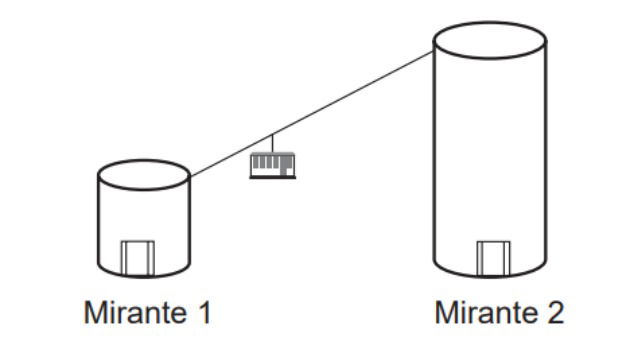
O acesso aos elevadores tem os seguintes custos:
- Subir pelo elevador 1: R$ 0,15;
- Subir pelo elevador 2: R$ 1,80;
- Descer pelo elevador 1: R$ 0,10;
- Descer pelo elevador 2: R$ 2,30.
O custo da passagem do teleférico partindo do topo do mirante 1 para o topo do mirante 2 é de R$ 2,00, e do topo do mirante 2 para o topo do mirante 1 é de R$ 2,50.
Qual é o menor custo, em real, para uma pessoa visitar os topos dos dois mirantes e retornar ao solo?
a) 2,25
b) 3,90
c) 4,35
d) 4,40
e) 4,45
4. Geometria espacial
Identificar os sólidos geométricos sejam eles poliedros ou sólidos de revolução e saber aplicar os conceitos da geometria plana para entender a geometria espacial são habilidades fundamentais. Isso porque esses conteúdos aparecem com frequência nas provas, tornando essencial o domínio desse tema.
Além disso, podem aparecer questões que envolvam uma visão espacial, planificações, teorema de Pitágoras e cálculo de perímetro.
Questão 4
(Enem - 2017) Um garçom precisa escolher uma bandeja de base retangular para servir quatro taças de espumante que precisam ser dispostas em uma única fileira, paralela ao lado maior da bandeja, e com suas bases totalmente apoiadas na bandeja. A base e a borda superior das taças são círculos de raio 4 cm e 5 cm, respectivamente.

A bandeja a ser escolhida deverá ter uma área mínima, em centímetro quadrado, igual a
a) 192.
b) 300.
c) 304.
d) 320.
e) 400.
5. Funções
Na prova é cobrado com frequência função afim, função quadrática, função Exponencial e função logarítmica, além da lei de formação de uma função e o seu gráfico. Esse assunto é um dos mais importantes, pois está associado a diversas áreas do conhecimento.
Questão 5
(Enem - 2017) Para realizar a viagem dos sonhos, uma pessoa precisava fazer um empréstimo no valor de R$ 5 000,00. Para pagar as prestações, dispõe de, no máximo, R$ 400,00 mensais. Para esse valor de empréstimo, o valor da prestação (P) é calculado em função do número de prestações (n) segundo a fórmula
Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335.
De acordo com a fórmula dada, o menor número de parcelas cujos valores não comprometem o limite definido pela pessoa é pela pessoa é
a) 12.
b) 14.
c) 15.
d) 16.
e) 17.
Para mais exercícios de função, veja também:
- Exercícios de Função Afim
- Função Quadrática - Exercícios
- Função Exponencial - Exercícios
- Logaritmo - Exercícios
6. Probabilidade
Para esse conteúdo não basta apena saber as fórmulas de probabilidade, é fundamental saber aplicá-las dentro do contexto proposto no enunciado.
Questão 6
(Enem - 2017) Um morador da região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima de 30% a probabilidade da ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
a) 0,075
b) 0,150
c) 0,325
d) 0,600
e) 0,800
Função, logaritmo, probabilidade... Parecem difíceis? Com o Toda Matéria+, você tem acesso a questões inéditas explicadas passo a passo, simulados com temas organizados e dicas práticas para resolver até as questões mais complexas. Você não precisa decorar, precisa entender. E a gente te ajuda nisso!
7. Geometria plana
Geometria Plana é fundamental no ENEM, pois aparece em questões sobre áreas, perímetros, ângulos e figuras do cotidiano, como pisos e terrenos. Mais do que saber fórmulas, é preciso compreender os conceitos e interpretar os problemas usando raciocínio lógico e visualização espacial. Dominar essa matéria facilita resolver questões práticas e fortalece a resolução de problemas reais.
Questão 7
Para estimar a quantidade de tijolos a ser usada na construção de uma parede, é necessário saber como o tijolo será assentado, pois a estimativa depende de qual face do tijolo ficará aparente na parede.
Em uma obra, um pedreiro deverá construir uma parede, na qual haverá uma janela, ambas em formato retangular, utilizando tijolos em forma de blocos de faces também retangulares, com as medidas indicadas na figura a seguir.
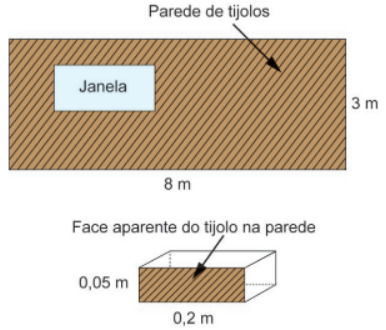
Segundo as orientações que recebeu, a janela não poderá ser tão pequena a ponto de a medida de sua área equivaler à área da face aparente de 100 tijolos, e nem tão grande a ponto de ocupar uma área de medida maior ou igual a 1/6 da medida da área da parede, na situação em que não houvesse janela na parede. Despreze a espessura da massa para assentar esses tijolos.
Nessas condições, as quantidades mínima e máxima de tijolos que poderão ser utilizados na construção dessa parede são, respectivamente,
a) 100 a 400
b) 100 a 2400
c) 2000 a 2300
d) 733 a 2396
e) 2500 a 2800
A parede tem 24 metros quadrados (3 m × 8 m) e cada tijolo tem área aparente de 0,01 m² (0,05 m × 0,2 m). Sem janela, seriam usados 2400 tijolos. Como a janela deve ter área maior que a de 100 tijolos (1 m²) e menor que 1/6 da parede (4 m²), a área útil da parede varia entre 20 m² e 23 m². Assim, a quantidade mínima de tijolos (com janela maior) é 2000 e a máxima (com janela menor) é 2300, correspondendo à alternativa C.
8. Combinatória
A Análise Combinatória é importante no ENEM porque ajuda a resolver problemas de contagem, organização e agrupamento em situações do dia a dia. Ela permite calcular possibilidades em contextos variados, como grupos e sequências, que são comuns em questões de probabilidade e estatística. Dominar esse assunto desenvolve o raciocínio lógico e a capacidade de aplicar a matemática em problemas reais.
Questão 8
Para abrir a porta de uma empresa, cada funcionário deve cadastrar uma senha utilizando um teclado alfanumérico como o representado na figura.

Por exemplo: a tecla que contém o número 2 traz as letras correlacionadas A, B e C. Cada toque nessa tecla mostra, sequencialmente, os seguintes caracteres: 2, A, B e C. Para os próximos toques, essa sequência se repete. As demais teclas funcionam da mesma maneira.
As senhas a serem cadastradas pelos funcionários devem conter 5 caracteres, sendo 2 algarismos distintos seguidos de 3 letras diferentes, nessa ordem. Um funcionário irá cadastrar a sua primeira senha, podendo escolher entre as teclas que apresentam os números 1, 2, 5, 7 e 0 e as respectivas letras correlacionadas, quando houver.
O número de possibilidades diferentes que esse funcionário tem para cadastrar sua senha é
a) 11520
b) 14400
c) 18000
d) 312000
e) 390000
Algarismos (2 dígitos distintos):
Teclas disponíveis: 1, 2, 5, 7, 0 (5 opções).
Combinações: 5×4=20 (pois os dígitos devem ser diferentes).
Letras (3 letras diferentes):
Letras disponíveis: A, B, C, J, K, L, P, Q, R, S (10 opções).
Combinações: 10×9×8=720 (letras distintas).
Total de senhas:
20×720=14.40020×720=14.400.
Resposta: B) 14.400.
9. Matrizes
Matrizes são úteis no ENEM porque facilitam a organização e resolução de problemas com sistemas lineares, tabelas e dados. Elas aparecem em várias disciplinas e situações do dia a dia. Saber operações básicas, como soma e multiplicação, ajuda na análise e interpretação de informações. Além disso, matrizes se relacionam com geometria e estatística, tornando-se importantes em questões interdisciplinares e desenvolvendo o raciocínio lógico.
Questão 9
Os candidatos A, B e C participaram de um concurso composto por uma prova de Matemática, uma de Português e outra de Geografia, sendo os pesos dessas três provas diferentes. As notas obtidas por esses três candidatos e os pesos atribuídos a essas provas estão representados nas tabelas:
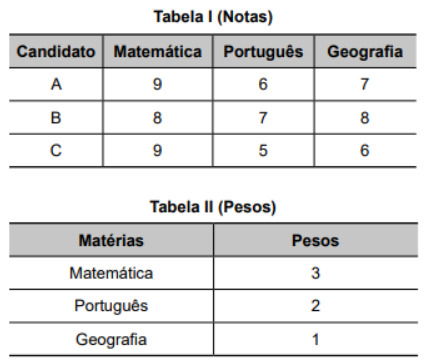
As notas finais são obtidas somando-se os produtos das notas pelos respectivos pesos. As notas finais dos três candidatos podem ser obtidas multiplicando-se a matriz das notas dos três candidatos nas três provas pela matriz dos pesos das três provas.
A matriz das notas finais dos três candidatos é
a)
b)
c)
d)
e)
Vamos calcular as notas finais dos candidatos, multiplicando as notas pelos pesos correspondentes conforme indicado nas tabelas:
Pesos:
Matemática: 3
Português: 2
Geografia: 1
Candidato A
Nota final = (9 × 3) + (6 × 2) + (7 × 1)
Nota final = 27 + 12 + 7 = 46
Candidato B
Nota final = (8 × 3) + (7 × 2) + (8 × 1)
Nota final = 24 + 14 + 8 = 46
Candidato C
Nota final = (9 × 3) + (5 × 2) + (6 × 1)
Nota final = 27 + 10 + 6 = 43
As notas finais dos candidatos são:
A: 46
B: 46
C: 43
A matriz das notas finais é:
10. Trigonometria
A trigonometria é importante no ENEM porque ajuda a resolver problemas práticos com medições, distâncias e ângulos. Ela aparece em situações reais, como calcular alturas ou trajetórias, e se conecta a outros temas da prova. Entender seno, cosseno e tangente melhora o raciocínio lógico e facilita resolver questões interdisciplinares.
Questão 10
Na modelagem e no estudo de fenômenos periódicos, em geral, os modelos associados fazem uso de funções trigonométricas. Nesse sentido, considere um experimento, realizado em laboratório, em que uma planta foi colocada em uma estufa, onde a temperatura é controlável. O experimento consiste em observar alterações nas características dessa planta ao ser submetida a variações de temperatura. Durante 24 horas, a temperatura da estufa variou de acordo com a função
em que
é medido em hora, variando no intervalo
.
Durante esse experimento, quantas vezes a temperatura na estufa atingiu o seu valor mínimo?
a) 1
b) 3
c) 4
d) 5
e) 7
A função é periódica, com base na função seno.
A parte sen(πx/4) tem período 8, pois o período do seno é 2π, então:
πx/4 = 2π → x = 8.
Ou seja, a temperatura completa um ciclo a cada 8 horas.
Em 24 horas, temos:
24 ÷ 8 = 3 ciclos completos.
O valor mínimo da função T(x) ocorre quando sen(πx/4) = 1, pois:
T(x) = 20 - 10(1) = 10, que é o valor mínimo.
O seno vale 1 a cada ciclo, uma vez por ciclo.
Quiz de Matemática Enem
Dicas para ir bem na prova de Matemática
A prova de Matemática é composta por questões de diferentes níveis de dificuldade e é obvio que quanto mais questões o aluno resolver sem "chutar" melhor.
Desta forma, o ideal é fazer as questões mais fáceis primeiro. Assim, o estudante assegurará que não deixará de acertar essas questões por não ter tido tempo de fazê-las.
As questões, por serem contextualizadas, normalmente são muito extensas. Então, uma dica é sublinhar as informações mais importantes, desta forma evita-se ler várias vezes a mesma questão.
Os gráficos, tabelas e infográficos aparecem com muita frequência na prova. Muitas vezes, a correta interpretação desses recursos é suficiente para acertar a questão.
Assim, antes de tirar conclusões precipitadas, observe as grandezas envolvidas olhando os eixos, identifique as escalas e unidades usadas e veja o seu título. Tudo isso pode fazer uma grande diferença nesse tipo de questão.
Como a prova possui muitas questões e pouco tempo para a sua resolução, o aluno deverá, sempre que possível, simplificar os cálculos.
Para ganhar minutos preciosos poderá, por exemplo, aplicar produtos notáveis em potenciações, fazer aproximações, estimativas e cálculo mental, substituir números muito grandes por potências de 10 e simplificar frações.
Leia também sobre:
Como se preparar para ir bem na prova de Matemática
Para começar, faça as pazes com essa matéria. Muitos alunos criam uma relação muito ruim com a Matemática e acabam acreditando que nunca conseguirão ter um bom desempenho nesta disciplina.
Ter essa crença só dificultará o seu aprendizado e portanto, deixe-se envolver com os encantos dos números! Acredite, você pode realmente aprender Matemática e corre ainda o risco de acabar gostando.
Para isso, comece a se preparar fazendo uma revisão dos conteúdos do ensino fundamental. Esses conteúdos, além de serem a base para o aprendizado, são também cobrados no Enem.

Crie o hábito de resolver os exercícios sem usar a calculadora. Não é permitido o seu uso na prova e sem saber fazer as operações fundamentais será muito difícil tem um bom desempenho.
Além disso, procure aprender técnicas que facilitam as contas, pois o tempo tem um peso muito grande nesta prova.
Uma boa sugestão é anotar quantos minutos leva para fazer cada questão e ir tentando sempre fazer em um menor tempo.
O ponto de partida para resolver uma questão de Matemática é a interpretação. Principalmente no Enem, onde as questões são contextualizadas, entender o enunciado é fundamental.
Desta forma, ler todos os dias textos dos mais variados temas, não só de Matemática, podem ajudar a melhorar a leitura e interpretação.
E por último, mas não menos importante, faça exercícios. Procure se familiarizar com o formato das questões do Enem, resolvendo provas de anos anteriores.
Procure resolver as questões sozinho primeiro. Se não conseguir resolver, não olhe imediatamente o gabarito. Tente novamente depois de um tempo, ser perseverante é fundamental.
Conforme for acertando as questões que fizer sozinho, ganhará mais confiança e passará a gostar mais de aprender Matemática, garanto.
Você não precisa ser “bom em Matemática” — só precisa da orientação certa. No Toda Matéria+, você encontra um caminho claro:
- Conteúdo por assunto do Enem
- Exercícios com gabarito explicado por professores
- Simulados, resumos e estratégias para cada tipo de questão
É o apoio que faltava para você transformar o jeito como estuda.
Leia também
assuntos que mais caem no Enem
o que estudar para o ENEM 2025 e tirar nota 1000
e prepare-se melhor para o dia da prova com estes exercícios e simulados, aliados poderosos para quem vai fazer o Enem este ano:
Questões de Matemática no Enem
Simulado de Matemática e suas Tecnologias (ENEM)
Simulado de Matemática e suas Tecnologias (ENEM 2024)
Simulado de Matemática e suas Tecnologias (ENEM 2023)
GOUVEIA, Rosimar. Matemática no Enem 2025: os conteúdos que mais caem. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/matematica-no-enem/. Acesso em:



