Exercícios sobre transformações trigonométricas (com gabarito explicado)
As transformações trigonométricas são ferramentas que permitem simplificar expressões e resolver equações que envolvem funções trigonométricas. Faça as questões abaixo e teste os seus conhecimentos sobre o assunto.
Questão 1
Qual o valor da expressão ?
a)
b)
c)
d)
Uma forma de resolver esta questão é aplicarmos diretamente a expressão do seno do arco duplo.
Questão 2
A expressão , para todo
, é equivalente a:
a)
b)
c)
d)
Dado vamos trabalhar numerador e denominador.
Questão 3
Qual o valor da expressão ?
a)
b)
c)
d)
Para resolver esta questão, primeiro, aplicamos a transformação de soma em produto no numerador:
Observe tambem que podemos aplicar a seguinte identidade trigonométrica no denominador:
Portanto,
Questão 4
Simplifique a expressão . Qual o valor de
?
a)
b)
c)
d)
Utilizando as identidades para redução ao primeiro quadrante temos:
Substituindo tais relações:
Questão 5
Qual o valor da expressão?
a)
b)
c)
d)
Elevando ambos os membros ao quadrado temos:
Agora calculamos o valor do seno de 75º usando a expressão do seno da soma.
Substituindo na expressão que obtemos anteriormente:
Mas, como os arcos da expressão inicial pertencem ao primeiro quadrante os valores de seno e cosseno são positivos, portanto, a solução é:
Questão 6
Qual o valor máximo que assume, dado que
?
a)
b)
c)
d)
Podemos transformar a soma das funções trigonométricas em uma única função tratando os coeficientes como lados de um triângulo retângulo.
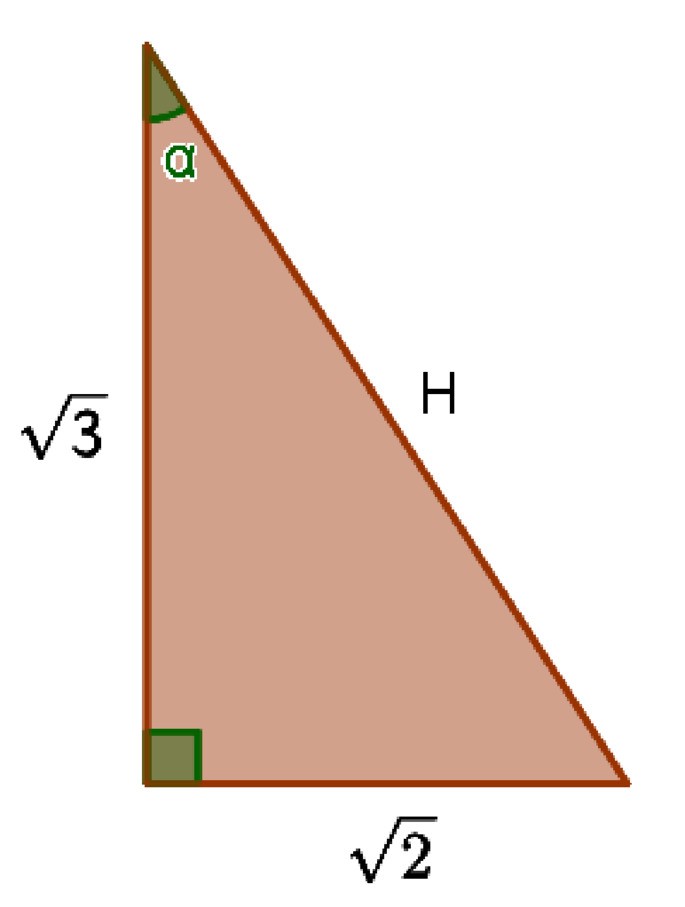
Podemos reescrever os radicais em função de seno e cosseno de .
Substituindo na expressão original:
Como a função cosseno assume valor máximo igual a , o valor máximo da expressão será
.
Questão 7
Quantas são as soluções da equação , no intervalo
?
a) 3
b) 4
c) 5
d) 6
Aplicando a transformação de soma em produto teremos:
Então,
Portanto, teremos 6 soluções no intervalo proposto.
Questão 8
O valor de ?
a)
b)
c)
Fazendo,
A nossa expressão pode ser reescrita como:
Aprofunde os seus estudos:
Referências Bibliográficas
DANTE, Luiz Roberto. Matemática: contexto e aplicações – volume único. 3. ed. São Paulo: Ática, 2016.
IEZZI, Gelson. Fundamentos de matemática elementar – volume 3: trigonometria. 9. ed. São Paulo: Atual, 2013.
MORGADO, Augusto César; DO CARMO, Manfredo Perdigão; WAGNER, Eduardo. Trigonometria e números complexos. 3. ed. São Paulo: SBM, 2005.
PAIVA, Manoel Rodrigues. Matemática – volume único. 3. ed. São Paulo: Moderna, 2010.
Exercícios sobre transformações trigonométricas (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-transformacoes-trigonometricas-com-gabarito-explicado/. Acesso em:

