Exercícios sobre transformações cíclicas da termodinâmica (com gabarito)
As transformações cíclicas da Termodinâmica estão presentes em diversos dispositivos do nosso dia a dia, como motores, usinas e refrigeradores. Compreender esses processos é fundamental para entender como a energia é convertida, transferida e aproveitada em forma de trabalho útil.
Confira as questões no estilo ENEM, acompanhadas de gabarito comentado, que vão ajudá-lo(a) a revisar conceitos, praticar cálculos e consolidar seu aprendizado sobre ciclos termodinâmicos. Resolva os exercícios e teste seus conhecimentos!
Questão 1
Os refrigeradores são eletrodomésticos essenciais no cotidiano moderno, responsáveis pela conservação de alimentos. Seu funcionamento se baseia em um ciclo termodinâmico realizado por um fluido refrigerante, que circula em um sistema fechado. O motor (compressor) do refrigerador realiza trabalho sobre esse fluido para que ele possa "bombear" calor de uma fonte fria (o interior do aparelho) para uma fonte quente (o ambiente externo, através da grade na parte de trás do equipamento). O Selo PROCEL de Economia de Energia classifica esses aparelhos com base em sua eficiência, ou seja, na sua capacidade de retirar calor gastando o mínimo de energia elétrica.
O diagrama Pressão (P) versus Volume (V) a seguir representa de forma simplificada as transformações sofridas pelo fluido refrigerante em um ciclo.
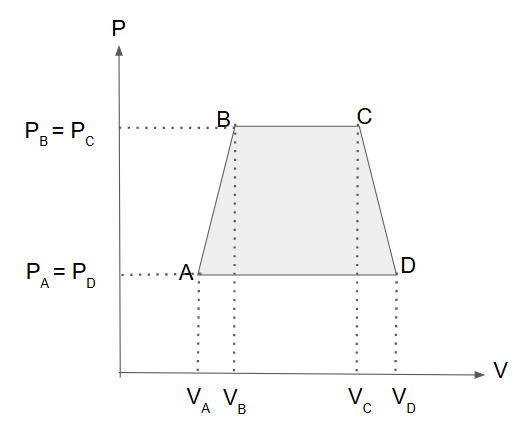
Em cada ciclo completo, o motor realiza um trabalho de 1200 J sobre o gás, e o calor total liberado para o ambiente na serpentina traseira é de 4000 J.
Considerando um ciclo completo do processo descrito, a quantidade de calor que esse refrigerador consegue retirar de seu interior (a fonte fria) é de:
a) 1200 J
b) 2800 J
c) 4000 J
d) 5200 J
Resposta correta: alternativa b) 2800 J
Vamos primeiro aplicar a Primeira Lei da Termodinâmica para um ciclo completo. Ela diz que o sistema (o fluido refrigerante) retorna ao seu estado inicial, o que significa que sua variação de energia interna (ΔU) é zero.
A lei afirma que ΔU = Q - W.
Como ΔU = 0 para um ciclo, temos que Q = W.
Aqui, Q é o calor total trocado no ciclo, e W é o trabalho total.
O problema afirma que o motor realiza um trabalho de 1200 J sobre o gás. Pela convenção termodinâmica, quando o trabalho é realizado sobre o sistema, ele é negativo. Portanto, W = - 1200 J.
O calor total é a soma do calor absorvido da fonte fria (Qfrio, que é positivo, pois entra no sistema) e o calor liberado para a fonte quente (Qquente, que é negativo, pois sai do sistema).
Qtotal = Qfrio + Qquente
O enunciado diz que o calor liberado é de 4000 J, então Qquente = - 4000 J.
Substituindo os valores na equação do ciclo (Q = W):
Qfrio + Qquente = W
Qfrio + ( - 4000 J) = - 1200 J
Qfrio - 4000 J = - 1200 J
Qfrio = 4000 J - 1200 J
Qfrio = 2800 J
Questão 2
As usinas termelétricas são uma parte importante da matriz energética de muitos países. Elas funcionam convertendo a energia térmica, liberada pela queima de combustíveis como carvão ou gás natural, em trabalho mecânico e, subsequentemente, em energia elétrica. O princípio de funcionamento é o de uma máquina térmica que opera em um ciclo.
Em uma usina simplificada, a queima do combustível aquece a água em uma caldeira, produzindo vapor a alta pressão. Esse vapor se expande e gira uma turbina (realizando trabalho), que aciona um gerador. Após passar pela turbina, o vapor é resfriado em um condensador, geralmente utilizando a água de um rio ou do mar (fonte fria), para que possa retornar à caldeira e reiniciar o ciclo.
O diagrama a seguir ilustra o fluxo de energia em uma dessas usinas. Para cada ciclo de operação, a usina absorve 200 Megajoules (MJ) de energia na forma de calor da queima do combustível e libera 120 MJ de calor para o rio que atua como fonte fria.
Diagrama de Fluxo de Energia:
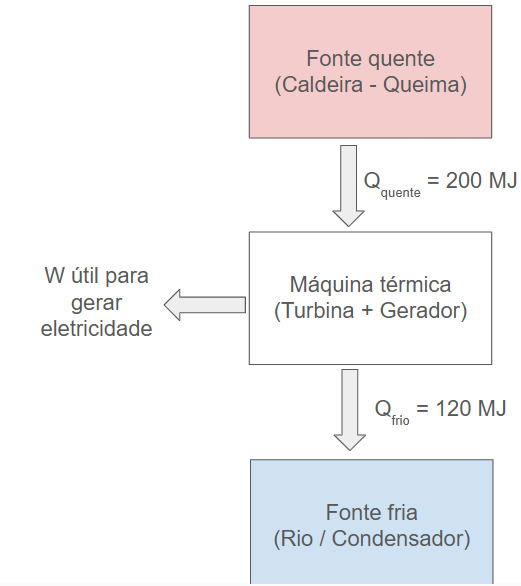
Com base no ciclo termodinâmico descrito e nos dados fornecidos, a eficiência energética desta usina termelétrica é de:
a) 100%
b) 80%
c) 60%
d) 40%
Resposta correta: alternativa d) 40%
A eficiência é a razão entre a energia útil que a máquina produz (o trabalho, W) e a energia total que ela consome da fonte quente (Qquente) para funcionar, ou:
η = W / Qquente
O trabalho útil (W) realizado pela máquina não é dado diretamente, mas pode ser calculado usando a Primeira Lei da Termodinâmica aplicada a um ciclo pela conservação de energia.
A energia que entra na máquina (Qquente) é convertida em duas partes: uma parte vira trabalho útil (W) e a outra é inevitavelmente perdida como calor para a fonte fria (Qfrio).
Pela balanço de Energia, vem:
Qquente = W + Qfrio
W = Qquente - Qfrio
Substituindo os valores dados no enunciado, ficamos com:
W = 200 MJ - 120 MJ
W = 80 MJ
Agora que temos o trabalho (W = 80 MJ) e o calor da fonte quente (Qquente = 200 MJ), podemos usar a fórmula da eficiência. Temos:
η = W / Qquente
η = 80 MJ / 200 MJ
η = 8 / 20
η = 0,40 ou 40%
Questão 3
No século XIX, o engenheiro francês Sadi Carnot, em seus estudos sobre a eficiência dos motores a vapor, idealizou um ciclo termodinâmico teórico reversível, conhecido hoje como Ciclo de Carnot. Este ciclo representa o limite máximo de eficiência que qualquer máquina térmica pode atingir ao operar entre duas fontes de calor, uma quente e uma fria. A eficiência de uma máquina de Carnot depende exclusivamente das temperaturas absolutas (em Kelvin) dessas duas fontes.
Um engenheiro projeta uma usina geotérmica que utiliza o vapor dʼágua de um reservatório subterrâneo como fonte quente e a água de um rio como fonte fria.
As temperaturas de operação são:
Fonte Quente (Tquente): 227 °C
Fonte Fria (Tfria): 27 °C
Considere: Temperatura em Kelvin (K) = Temperatura em Celsius (°C) + 273.
Analise cada uma das seguintes afirmações sobre a usina projetada e classifique-a como Verdadeira (V) ou Falsa (F). Depois marque a alternativa correta.
I. A máxima eficiência teórica que qualquer máquina térmica poderia atingir operando entre as temperaturas fornecidas é de 40%.
II. Se, após a construção, a usina real apresentar uma eficiência de 50%, isso representaria um grande avanço tecnológico, superando as previsões teóricas de Carnot.
III. Para aumentar a eficiência teórica máxima do projeto, uma das estratégias possíveis seria perfurar mais fundo para encontrar uma fonte de vapor mais quente, mantendo a mesma temperatura da fonte fria.
a) F, V, F
b) V, V, V
c) F, F, V
d) V, F, V
Resposta correta: alternativa d) V, F, V
Análise da frase I: A máxima eficiência teórica é dada pela eficiência do ciclo de Carnot, que se calcula com a fórmula η = 1 - (Tfria / Tquente). As temperaturas devem estar na escala absoluta (Kelvin).
Primeiro vamos converter as temperaturas para Kelvin:
Tquente = 227 °C + 273 = 500 K
Tfria = 27 °C + 273 = 300 K
Vamos agora aplicar a fórmula da eficiência de Carnot:
ηmax = 1 - (300 K / 500 K)
ηmax = 1 - 0,6
ηmax = 0,4 ou 40%
Conclusão: A frase I está correta.
Análise da frase II: A Segunda Lei da Termodinâmica, expressa pelo trabalho de Carnot, estabelece que nenhuma máquina térmica real operando entre duas fontes de calor pode ser mais eficiente do que uma máquina de Carnot operando entre as mesmas duas fontes.
A eficiência máxima teórica (Carnot) calculada no item I é de 40%.
A afirmação propõe uma usina real com eficiência de 50%.
Como 50% > 40%, uma máquina com essa eficiência é impossível segundo as leis da física. Ela não "superaria" as previsões de Carnot; ela as violaria.
Conclusão: A frase está portanto incorreta, pois descreve uma situação fisicamente impossível.
Análise da frase III: Devemos analisar como a eficiência teórica máxima (ηmax = 1 - Tfria / Tquente) é afetada pela mudança na temperatura da fonte quente.
Para aumentar o valor de ηmax, o termo (Tfria / Tquente) deve diminuir. Se mantivermos Tfria constante e aumentarmos Tquente, o valor da fração diminuirá. Consequentemente, o valor de (1 - fração) aumentará, elevando a eficiência.
A estratégia de "encontrar uma fonte de vapor mais quente" corresponde exatamente a aumentar Tquente. Portanto, essa ação levaria a um aumento na eficiência teórica máxima possível para o sistema.
Conclusão: A frase está correta.
Questão 4
Os motores de combustão interna, que equipam a maioria dos automóveis, são máquinas térmicas que convertem a energia química liberada pela queima do combustível em trabalho mecânico. Este processo ocorre em ciclos repetitivos. Em uma aproximação do ciclo de Otto, que modela esses motores, pode-se considerar que a cada ciclo uma quantidade de calor (Q₁), proveniente da explosão da mistura ar-combustível, é fornecida ao gás na câmara de combustão, que se expande e realiza trabalho para mover os pistões.
Um motor de um carro popular opera com uma eficiência de 30% e, a cada ciclo, o calor absorvido da fonte quente (a queima do combustível) é de 4000 J. Em uma viagem por uma estrada plana, o motorista mantém uma rotação constante de 3000 RPM (rotações por minuto). É importante notar que, em um motor de quatro tempos como este, um ciclo termodinâmico completo que produz trabalho útil ocorre a cada duas rotações do virabrequim.
Nessas condições de operação, a potência útil, em quilowatts (kW), que o motor está desenvolvendo é de:
a) 60 kW
b) 100 kW
c) 30 kW
d) 200 kW
Resposta correta: alternativa c) 30 kW
Potência é a taxa de realização de trabalho, ou seja, a quantidade de trabalho realizado por unidade de tempo (Potência = Trabalho / tempo). Para resolver a questão, precisamos encontrar o trabalho útil realizado em cada ciclo e a frequência com que esses ciclos ocorrem.
A eficiência (η) de uma máquina térmica é a razão entre o trabalho útil (W) e o calor absorvido da fonte quente (Q₁), ou:
η = W / Q₁
Podemos rearranjar a expressão para isolar o trabalho: W = η . Q₁
Substituindo os valores dados no enunciado, temos:
η = 30% = 0,30
Q₁ = 4.000 J
W = 0,30 × 4.000 J
W = 1200 J
Este é o trabalho útil produzido em um ciclo completo.
A frequência é o número de ciclos que ocorrem por segundo. O motor opera a 3000 RPM (rotações por minuto). A informação crucial é que um ciclo ocorre a cada 2 rotações. Portanto:
Para encontrar a potência em Watts (Joules por segundo), precisamos da frequência em Hertz (ciclos por segundo).
f = 1500 ciclos / minuto = 1500 ciclos / 60 segundos
f = 25 ciclos/s ou 25 Hz
A potência é o trabalho realizado por ciclo multiplicado pelo número de ciclos por segundo, ou:
P = W . f
P = 1200 J/ciclo . 25 ciclos/s
P = 30000 J/s = 30000 W
A questão pede a resposta em quilowatts (kW). Como 1 kW = 1.000 W:
P = 30000 W / 1000
P = 30 kW
Questão 5
A crescente demanda por energia elétrica exige a construção de novas usinas. Uma das principais preocupações ambientais relacionadas às usinas termelétricas é a "poluição térmica", que ocorre quando a água utilizada para resfriar o sistema (a fonte fria) é devolvida a rios ou mares com uma temperatura elevada, podendo afetar ecossistemas aquáticos. A quantidade de calor rejeitado para o ambiente está diretamente ligada à eficiência da usina.
Uma cidade precisa instalar uma nova usina e avalia dois projetos distintos, A e B.
Projeto A: Propõe uma usina de tecnologia mais moderna, com uma eficiência energética ou rendimento de 40%.
Projeto B: Propõe uma usina de tecnologia mais convencional. Em cada ciclo, ela absorve 250 Megajoules (MJ) de calor da fonte quente e realiza um trabalho útil de 80 MJ.
Para avaliar o impacto ambiental comparativo, a equipe técnica decide calcular a quantidade de calor rejeitado para o ambiente para cada megajoule de energia elétrica útil gerada.
Qual é a diferença na quantidade de calor rejeitado (em MJ) por megajoule de trabalho útil entre a usina menos eficiente e a mais eficiente?
a) 0,625
b) 0,08
c) 0,50
d) 1,50
Resposta correta: alternativa a) 0,625
O objetivo é comparar o calor rejeitado (Qfrio) por unidade de trabalho útil (W) para cada usina.
1. Análise do Projeto A:
Eficiência (ηA) = 40% = 0,40.
A eficiência é definida como η = W / Qquente. Portanto, Qquente = W / η.
Pela Primeira Lei da Termodinâmica em um ciclo, o calor rejeitado (Qfrio) é a diferença entre o calor absorvido e o trabalho realizado: Qfrio = Qquente - W.
Substituindo Qquente na equação, temos:
Isso significa que, para cada 1 MJ de trabalho útil, a usina do Projeto A rejeita 1,5 MJ de calor.
2. Análise do Projeto B:
Primeiro vamos calcular a eficiência da usina B para poder compará-las.
ηB = WB / Qquente,B = 80 MJ / 250 MJ = 8 / 25 = 0,32 = 32%
Agora, calculamos o calor rejeitado (Qfrio,B) em um ciclo:
Qfrio,B = Qquente,B - WB = 250 MJ - 80 MJ = 170 MJ
A usina B rejeita 170 MJ de calor para cada 80 MJ de trabalho que realiza.
Precisamos encontrar a razão de calor rejeitado por MJ de trabalho:
Razão = Qfrio,B / WB = 170 MJ / 80 MJ = 17 / 8 = 2,125.
Isso significa que, para cada 1 MJ de trabalho útil, a Usina B rejeita 2,125 MJ de calor.
3. Comparação e Cálculo da Diferença:
A Usina A (η = 40%) é mais eficiente que a Usina B (η = 32%). Portanto, a Usina B é a menos eficiente.
Calor rejeitado por MJ de trabalho útil:
Usina A (mais eficiente): 1,50 MJ
Usina B (menos eficiente): 2,125 MJ
A questão pede a diferença entre a usina menos eficiente e a mais eficiente:
Diferença = (Calor rejeitado da B) - (Calor rejeitado da A)
Diferença = 2,125 MJ - 1,50 MJ = 0,625 MJ.
Questão 6
Engenheiros de um laboratório de pesquisa em biocombustíveis estão testando o desempenho de um novo motor experimental. Este motor utiliza um gás ideal que passa por um ciclo termodinâmico, conforme representado no diagrama P abaixo.
O ciclo é composto por três processos: uma expansão isobárica (A → B), um resfriamento isocórico (B → C) e uma compressão (C → A) que fecha o ciclo.
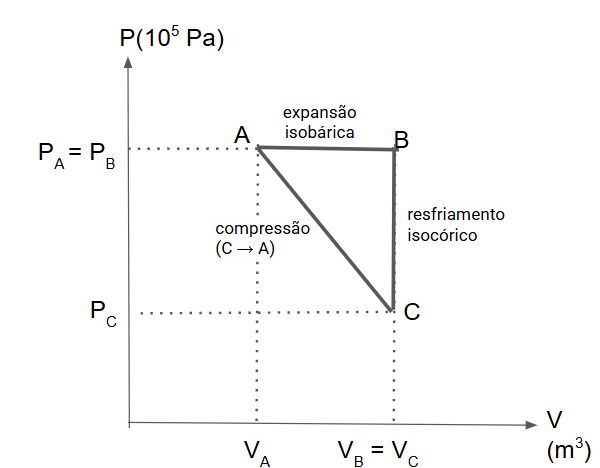
Durante a primeira etapa do ciclo, a expansão de A para B, o gás absorve uma quantidade de calor de 2500 kJ da queima do biocombustível.
Determine a variação da energia interna (ΔU) do gás durante o processo de expansão isobárica (A → B), sabendo que PA= PB= 6.105 Pa, PC = 2.105 Pa, VA = 2 m3, VB = VC = 5 m3.
a) 1800 kJ
b) 700 kJ
c) 2500 kJ
d) 600 kJ
Resposta correta: alternativa b) 700 kJ
A questão pede a variação da energia interna (ΔU) especificamente para o trecho A → B do ciclo. Para isso, devemos usar a Primeira Lei da Termodinâmica ou:
ΔU = Q - W.
Precisamos encontrar o calor trocado (Q) e o trabalho realizado (W) neste trecho.
O enunciado fornece diretamente o valor do calor absorvido pelo gás neste processo.
QAB = + 2500 kJ. Inserimos o sinal positivo para ressaltar que o gás absorve calor.
O trabalho total realizado por um gás em uma transformação pode ser calculado pela área sob a curva no diagrama PV.
O processo A → B é uma expansão isobárica, ou seja, a pressão constante.
Para um processo isobárico, o trabalho é dado por: W = P . ΔV
Consultando o gráfico, temos:
Pressão constante (P): 6.10⁵ Pa
Volume inicial (VA): 2 m³
Volume final (VB): 5 m³
Variação de Volume ΔV = VB - VA = 5 m³ - 2 m³ = 3 m³
Podemos agora calcular o trabalho:
WAB = (6 . 10⁵ Pa) . (3 m³) = 18 . 10⁵ J
Como 1 kJ = 1000 J, temos:
WAB = 1800 kJ. O sinal é positivo porque o gás se expandiu, ou seja, realizou trabalho.
Vamos calcular a Variação da Energia Interna (ΔU) no trecho A → B, aplicando a Primeira Lei da Termodinâmica com os valores que encontramos.
ΔUAB = QAB - WAB
ΔUAB = 2500 kJ - 1800 kJ = 700 kJ
Questão 7
Diferente dos motores a gasolina que utilizam uma vela de ignição, os motores a diesel funcionam com base no princípio da autoignição. Nesses motores, o ar na câmara de combustão é comprimido a uma pressão e temperatura tão elevadas que, quando o combustível diesel é injetado, ele inflama espontaneamente. Este processo pode ser modelado pelo Ciclo Diesel, que descreve as transformações termodinâmicas sofridas pelo gás (uma mistura de ar e combustível) dentro do motor.
Considere um ciclo Diesel ideal, operando com um gás perfeito, conforme esquematizado no diagrama Pressão (P) versus Volume (V).
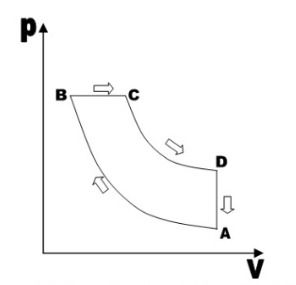
O ciclo consiste em quatro etapas:
A → B: Compressão adiabática.
B → C: Expansão isobárica (injeção e queima do combustível, fornecendo calor).
C → D: Expansão adiabática.
D → A: Resfriamento isocórico (liberação de calor).
Analise cada uma das afirmações a seguir como verdadeiras (V) ou falsas (F), e depois marque a alternativa correta.
I. Na etapa de compressão adiabática (A → B), a temperatura do gás aumenta significativamente, mesmo sem que ele receba calor de uma fonte externa.
II. O trabalho realizado pelo gás durante a expansão isobárica (B → C) é numericamente igual à quantidade de calor que ele absorve nesta mesma etapa.
III. O trabalho total realizado pelo motor em um ciclo completo, que corresponde à energia útil fornecida, é representado pela área interna delimitada pela trajetória A → B → C → D → A no diagrama PxV.
a) V, V, V
b) F, V, F
c) V, F, V
d) F, F, V
Resposta correta: alternativa c) V, F, V
Análise da frase I: A Primeira Lei da Termodinâmica afirma que a variação da energia interna (ΔU) de um sistema é ΔU = Q - W, onde Q é o calor trocado e W é o trabalho realizado.
Na compressão adiabática (A → B), por definição, não há troca de calor com o meio externo (Q = 0). O gás está sendo comprimido, o que significa que um trabalho está sendo realizado sobre ele. Pela convenção termodinâmica, o trabalho realizado pelo gás é negativo (W < 0).
Cálculo: ΔU = Q - W = 0 - W = -W. Como W é negativo, ΔU = - (um número negativo) = um número positivo.
Conclusão: A variação da energia interna (ΔU) é positiva. Como a energia interna de um gás ideal é diretamente proporcional à sua temperatura, um aumento na energia interna implica em um aumento na temperatura. Isso confirma o princípio da autoignição do motor a diesel. A frase está correta.
Análise da frase II: Novamente, usamos a Primeira Lei da Termodinâmica, ΔU = Q - W. Na etapa de expansão isobárica (B → C), o gás realiza trabalho ao se expandir (W > 0) e absorve calor da queima do combustível (Q > 0).
Para que o trabalho (W) fosse igual ao calor (Q), a variação da energia interna (ΔU) teria que ser zero. No entanto, em uma expansão isobárica onde calor é fornecido, a temperatura do gás também aumenta, o que significa que a energia interna também aumenta (ΔU > 0).
Rearranjando a fórmula para isolar o calor, temos:
Q = ΔU + W. Como ΔU > 0 e W > 0, o calor absorvido (Q) é necessariamente maior que o trabalho realizado (W). A energia do calor é usada parte para realizar trabalho e parte para aquecer o gás.
Conclusão: A frase está incorreta.
Análise da frase III: Este é um princípio fundamental da representação de ciclos termodinâmicos em diagramas PV.
Interpretação Gráfica:
- O trabalho realizado pelo gás durante a expansão (trechos B→C e C→D) é a área sob essa parte da curva.
- O trabalho realizado sobre o gás durante a compressão (trecho A→B) é a área sob essa curva.
- O trabalho líquido (ou total) do ciclo é a diferença entre o trabalho de expansão e o de compressão, que corresponde exatamente à área interna delimitada pelo ciclo.
Conclusão: A afirmação descreve corretamente como se calcula graficamente o trabalho útil de um ciclo termodinâmico. A frase está correta.
Para estudar mais: Transformações cíclicas da termodinâmica
Continue praticando com exercícios sobre termodinâmica (com respostas explicadas).
Exercícios sobre transformações cíclicas da termodinâmica (com gabarito). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-transformacoes-ciclicas-da-termodinamica-com-gabarito/. Acesso em:

