Exercícios sobre sólidos geométricos (com respostas explicadas)
Os sólidos geométricos fazem parte do estudo da Geometria Espacial e estão presentes em diversas situações do dia a dia, como construções, objetos e até na natureza. Entender suas propriedades é essencial para calcular áreas, volumes e resolver problemas aplicados.
Para ajudar na prática, reunimos uma lista de exercícios sobre sólidos geométricos, todos acompanhados de respostas explicadas, para que você possa revisar os conceitos e consolidar o aprendizado.
Questão 1
Uma anticlepsidra é um sólido geométrico obtido ao se remover dois cones idênticos, opostos pelo vértice, de um cilindro equilátero. Se o cilindro original tem altura H e raio da base R, e os cones removidos têm suas bases coincidentes com as bases do cilindro e seus vértices no centro do cilindro, qual a relação entre o volume da anticlepsidra e o volume de outro sólido?
a) O volume da anticlepsidra é 2/3 do volume de uma esfera de mesmo raio R.
b) O volume da anticlepsidra é 1/2 do volume de uma esfera de mesmo raio R.
c) O volume da anticlepsidra é igual ao volume de uma esfera de mesmo raio R.
d) O volume da anticlepsidra é 3/4 do volume do cilindro.
e) O volume da anticlepsidra é 4/3 do volume do cilindro.
Como o cilindro é equilátero temos que .
Precisamos calcular os volumes do cilindro, da clepsidra(dois cones) e da anticlepsidra(sólido que sobra ao retirar os cones.
Volume do Cilindro
Volume dos dois Cones (clepsidra)
Volume da Anticlepsidra
Que é exatamente o volume de uma esfera de raio R.
Questão 2
Um arquiteto está projetando um aquário em forma de ortoedro, cujas dimensões (comprimento, largura e altura) estão em progressão geométrica crescente.
A diagonal interna do aquário mede e a menor dimensão é igual a
.
Determine o volume desse aquário.
a) 72 cm³
b) 108 cm³
c) 162 cm³
d) 216 cm³
e) 324 cm³
A PG será dada por:
Aplicando a expressão para a diagonal de uma paralelepípedo reto retângulo (ortoedro) temos:
Dessa forma as dimensões do ortoedro são e seu volume será:
Questão 3
Um escultor deseja construir uma peça em formato de pirâmide regular hexagonal, utilizando vidro lapidado. Cada aresta da base mede e a altura da pirâmide é o dobro do raio da circunferência inscrita no hexágono da base.
Com base nessas informações qual será, respectivamente, o volume e a área total de vidro dessa pirâmide?
a)
b)
c)
d)
e)
O raio da circunferência inscrita na base é:
Como a altura é o dobro desse raio teremos:
Portanto o volume é dado por:
Aplicando o Teorema de Pitágoras para encontrar o apótema da pirâmide teremos:
Calculamos agora a área lateral:
Por fim, a área total:
Questão 4
Um fábrica de sorvetes produz casquinhas em forma de cone circular reto. Sabe-se que a geratriz da casquinha mede e que o ângulo central correspondente ao setor circular usado para montar a casquinha é de
. Qual é a área lateral da casquinha?
a)
b)
c)
d)
e)
O raio do setor circular é a geratriz do cone, portanto .
A área do setor em função do arco pode ser obtida por uma regra de três simples:
Questão 5
Uma esfera metálica foi moldada de forma que seu volume corresponde a . Se essa esfera for totalmente derretida e transformada em pequenos cubos de
de aresta, qual será o número máximo de cubos a ser obtido?
a) 108
b) 111
c) 112
d) 113
e) 114
O volume da esfera é aproximadamente:
Logo o número máximo de cubos será 113, pois mesmo que aumentemos a quantidade de casas decimais para o valor de , a partir de agora, nunca teremos parte inteira maior que 113.
Questão 6
Considere uma esfera de raio R em cujo interior se inscreve um cubo e no exterior se circunscreve um cubo
. Determine a razão entre os volumes de
e
.
a)
b)
c)
d)
e)
Cubo Inscrito: O diâmetro da esfera é igual a diagonal do cubo .
Cubo Circunscrito: O diâmetro da esfera é igual a aresta do cubo .
Calculamos agora a razão entre os volumes de e
.
Questão 7
Uma jarra em forma de tronco de cone reto tem as bases circulares com raios medindo e
. A altura da jarra é
. Sabendo que ela será totalmente preenchida com suco, qual será o volume de suco que a jarra comporta, em litros? Use
.
a) 4,8 L
b) 5,2 L
c) 6,1 L
d) 7,6 L
e) 8,4 L
O volume do tronco de cone é dado por:
Questão 8
Um cilindro circular reto tem altura . A base superior tem diâmetro AB; seja A uma extremidade desse diâmetro (ponto da borda superior). Um plano oblíquo corta o cilindro e contém o ponto A, conforme a figura abaixo.
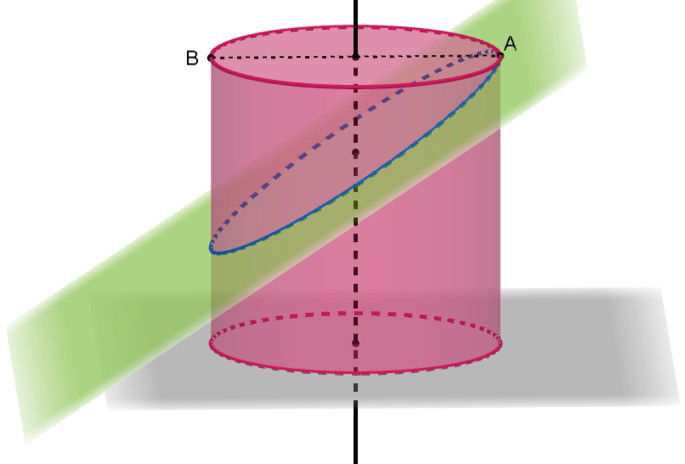
A interseção do plano com o cilindro é uma elipse cuja equação, no próprio plano de corte com a origem no centro da elipse e unidades em cm, é:
Determine o volume do maior dos dois sólidos obtidos após o corte.
a)
b)
c)
d)
e)
Observe que se traçarmos um plano paralelo a base a partir do ponto inferior do corte oblíquo teremos um cilindro pequeno abaixo e um cilindro grande acima. O volume do sólido procurado é igual ao volume do cilindro pequeno acrescido de metade do cilindro grande (pedaço).
Pela equação da elipse sabemos que semieixo menor vale e semieixo maior vale
.
Podemos também observar que o semieixo menor é igual ao diâmetro da base do cilindro e chamando de C o ponto de interseção do plano oblíquo com o cilindro na extremidade do eixo maior teremos um triângulo retângulo ABC, retângulo em B tal que:
Portanto, o cilindro pequeno tem altura 4 cm e o grande 8 cm.
Leia mais sobre sólidos geométricos e continue praticando com exercícios de Geometria Espacial (com questões resolvidas).
Referências Bibliográficas
DOLCE, Osvaldo; POMPEO, José Nicolau, Fundamentos de Matemática Elementar - Geometria Espacial, Volume 10 - 6ª Ed., São Paulo: Editora Atual, 2005.
PAIVA, Manoel Rodrigues, Matemática, 2 ed., São Paulo: Editora Moderna, 2010.
DANTE, Luiz Roberto, Matemática: contexto & aplicações: ensino médio, 3. ed. São Paulo: Ática, 2016.
Exercícios sobre sólidos geométricos (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-solidos-geometricos-com-respostas-explicadas/. Acesso em:

