Exercícios sobre plano inclinado

Resposta correta: alternativa b) 120 N

As forças que atuam no sistema são mostradas no esquema abaixo:

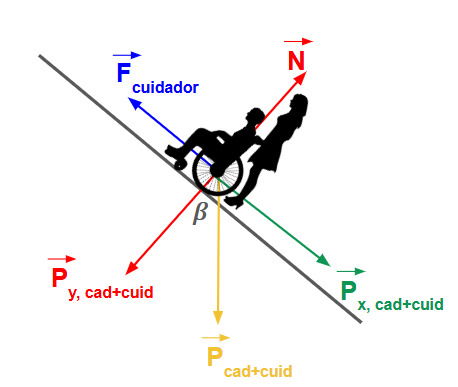
As forças presentes são:

• Força Peso (P): Atua verticalmente para baixo.
• Força Aplicada (F): Atua paralelamente à rampa, no sentido do movimento (para cima).
• Componente Paralela do Peso (P_x): É a projeção da força peso na direção do plano inclinado, "puxando" a cadeira para baixo.
• Componente Normal do Peso (P_y): É a projeção da força peso perpendicular ao plano, que é anulada pela Força Normal da rampa.

Vamos primeiro calcular a Força Peso (P):
P = massa × gravidade
P = 120 , 10 m/s²
P = 1200 N

Agora vamos calcular a Componente Paralela do Peso (P_x), lembrando que a fórmula para a componente paralela é P_y = P . sen(ß), onde ß é o ângulo de inclinação da rampa.
O problema não fornece o ângulo ß diretamente, mas nos dá as dimensões da rampa: o comprimento (hipotenusa = 12 m) e a altura (cateto oposto = 1,2 m).
Com esses dados, podemos calcular o seno do ângulo:
sen(ß) = Cateto Oposto / Hipotenusa
sen(ß) = 1,2 m / 12 m
sen(ß) = 0,1

Agora, calculamos Px:
Px = P . sen(ß)
Px = 1200 N . 0,1
Px = 120 N

Conclusão:
Como o movimento é com velocidade constante, a força aplicada pelo cuidador (F) deve anular a componente P_x. Portanto, F = P_y = 120 N.

Resposta correta: alternativa c) 300 N.

No esquema abaixo mostramos as forças presentes no sistema, temos:

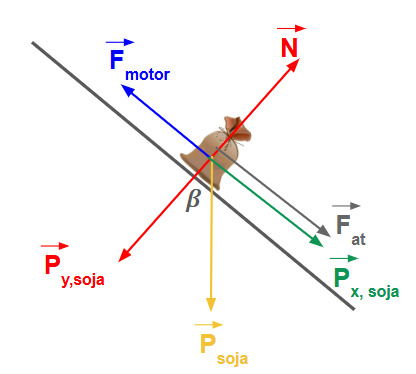
As forças que atuam na direção do movimento são:

• F_motor: A força aplicada pelo motor da esteira, para cima.
• F_at: A força de atrito (dissipativa), que se opõe ao movimento, logo, aponta para baixo ao longo da esteira.
• Pₓ: A componente tangencial da força peso, que naturalmente "puxa" o saco para baixo ao longo da esteira.

Para a força resultante ser nula, a força que impulsiona o movimento para cima deve anular a soma das forças que se opõem a ele, ou:

F_motor = Pₓ + F_at

Vamos calcular primeiro a força peso (P) pelo produto da massa pela aceleração da gravidade, ou:

P = m . g
P = 50 kg × 10 m/s²
P = 500 N

Vamos agora calcular a componente Pₓ do Peso, lembrando que a componente Pₓ é dada por Pₓ = P × sen(ß), onde ß é o ângulo de inclinação da esteira. O enunciado não fornece o ângulo, mas nos dá o comprimento da esteira (hipotenusa) e a altura que ela vence (cateto oposto ao ângulo ß).

• Cateto oposto = altura (h) = 10 m
• Hipotenusa = comprimento (L) = 20 m

Podemos calcular o seno do ângulo:

sen(ß) = cateto oposto / hipotenusa = h / L = 10 / 20 = 0,5

Agora, calculamos o valor de Pₓ:

Pₓ = P × sen(ß)
Pₓ = 500 N × 0,5
Pₓ = 250 N

Finalmente, para calcular a força do motor aplicamos a equação de equilíbrio de forças ou:
F_motor = Pₓ + F_at
F_motor = 250 N + 50 N
F_at = 300 N

A força que o motor precisa aplicar sobre cada saco de soja é de 300 N.

Resposta correta: alternativa d) 8000 N

O objetivo é manter o bloco em repouso (equilíbrio estático), pois o enunciado pede a força mínima para impedir que ele deslize. Isso significa que a força resultante sobre o bloco deve ser zero e que a força de atrito estático estará atuando em sua capacidade máxima para ajudar os trabalhadores, ou seja, apontando para cima na rampa, junto com a força dos trabalhadores.

No esquema abaixo mostramos as forças que agem no sistema:

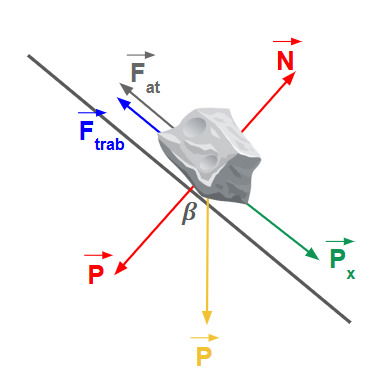
As forças que atuam na direção da rampa são:

Pₓ: A componente do peso que puxa o bloco para baixo, ao longo da rampa.

F_trab: A força aplicada pelos trabalhadores para cima, ao longo da rampa.

Fₐₜ: A força de atrito estático, que se opõe à tendência de movimento (que é para baixo). Portanto, a Fₐₜ também aponta para cima na rampa.

Na condição de equilíbrio a soma das forças para cima deve ser igual à força para baixo, ou:

F_trab + Fₐₜ = Pₓ

A força mínima dos trabalhadores (F_mín) ocorre quando o atrito é máximo (Fₐₜ,_max), ou:

F_mín = Pₓ - Fₐₜ,_max

O enunciado não traz o ângulo de inclinação da rampa, mas nos dá os catetos do triângulo retângulo que a forma onde o cateto oposto (altura) h = 6 m e cateto adjacente (base) b = 8 m.

Precisamos da hipotenusa (L) para encontrar o seno e o cosseno do ângulo de inclinação (ß). Para encontrá-la basta usar o Teorema de Pitágoras:

L² = h² + b²

L² = 6² + 8² = 36 + 64 = 100

L = 10 m

Agora, podemos calcular o seno e o cosseno:

sen(ß) = h / L = 6 / 10 = 0,6

cos(ß) = b / L = 8 / 10 = 0,8

Vamos agora calcular a Força Peso (P) e suas componentes (Pₓ e Pᵧ):

Massa (m) = 2,0 toneladas = 2000 kg.

Peso (P) = m . g = 2000 . 10 = 20000 N.

Componente Pₓ = P . sen(ß) = 20000 . 0,6 = 12000 N

Componente Pᵧ = P . cos(ß) = 20000 . 0,8 = 16000 N

Cálculo da Força de Atrito Estático Máxima (Fₐₜ, _max): a força normal (N) é igual em módulo à componente Pᵧ, pois não há movimento na direção perpendicular à rampa, ou:

N = Pᵧ = 16000 N.

A força de atrito estático máxima é:

Fₐₜ, _max = μₑ . N = 0,25 . 16000 N

Fₐₜ, _max = 4000 N

Por fim, vamos calcular a força mínima dos trabalhadores usando a equação de equilíbrio:

F_mín = Pₓ - Fₐₜ, _max

F_mín = 12000 - 4000

F_mín = 8000 N

Resposta correta: alternativa c) 4,13 m/s²

O problema pede para calcular a aceleração do esquiador que desce um plano inclinado. Como há aceleração, a força resultante não é nula. Para encontrar a aceleração teremos que aplicar a Segunda Lei de Newton que diz que Fᵣ = m . a

O esquema abaixo mostra as forças atuantesno sistema:

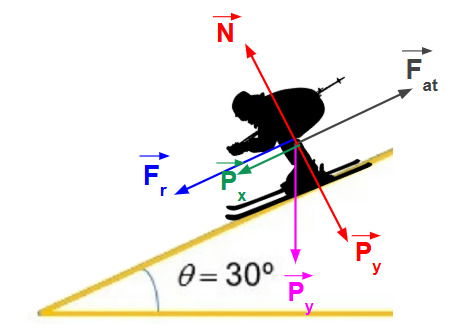
- A força peso (P) aponta verticalmente para baixo e precisa ser decomposta em suas duas componentes:

• Pₓ: componente paralela à pista, que "puxa" o esquiador para baixo.
• Pᵧ: componente perpendicular à pista, que pressiona o esquiador contra a neve.

- Força Normal (N): a força de reação da pista sobre o esquiador, perpendicular à superfície e apontando para cima. Ela se equilibra com Pᵧ, pois o esquiador não se movimenta nessa direção.

- Força de Atrito Cinético (Fₐₜ): força que se opõe-se ao movimento. Como o esquiador está descendo, a Fₐₜ aponta para cima, ao longo da pista.

Primeiro vamos calcular a Força Peso e suas componentes:

Peso (P) = m . g = 80 . 10 = 800 N

Componente Pₓ = P . sen(30°) = 800 . 0,50 = 400 N

Componente Pᵧ = P . cos(30°) = 800 . 0,87 = 696 N

Agora vamos calcular a Força de Atrito. Para isso, devemos primeiro determinar a Força Normal (N), pois a Força de Atrito é dada por Fₐₜ = μc . N.

Como não há movimento na direção perpendicular à pista, N = Pᵧ. Assim:

N = 696 N

Agora podemos calcular a Força de Atrito Cinético (Fₐₜ):

Fₐₜ = μ_c . N = 0,10 . 696 = 69,6 N. Esta é a força que freia o esquiador.

Vamos então, calcular a Força Resultante (Fᵣ). Lembre que a força resultante na direção do movimento é a diferença entre a força que acelera (Pₓ) e a força que freia (Fₐₜ) o esquiador, ou:

Fᵣ = Pₓ - Fₐₜ

Fᵣ = 400 - 69,6 = 330,4 N

Podemos agora calcular a aceleração (a), usando a Segunda Lei de Newton, temos:

a = Fᵣ / m

a = 330,4 / 80

a ≈ 4,13 m/s²

Resposta correta: alternativa b) 720 J

A questão pede o trabalho das forças dissipativas (Wₐₜ). Isso indica que a energia mecânica do sistema não se conserva. A melhor ferramenta para resolver este problema é o Teorema da Energia Cinética ou, de forma equivalente, o balanço de energia mecânica.

O teorema diz que o trabalho total realizado sobre um corpo é igual à variação de sua energia cinética (ΔE_c), ou: W_total = ΔE_c

O trabalho total é a soma do trabalho da força peso (W_peso) e do trabalho das forças dissipativas (W_at), ou: ΔE_c = W_peso + W_at

Podemos reescrever essa equação como: W_at = ΔE_c - W_peso

Podemos usar a conservação de energia para resolver esse problema. Ele diz que o trabalho é igual à diferença da energia mecânica final e inicial, ou:

W_at = E_mf - E_mi

Vamos primeiro determinar a Energia Mecânica Inicial E_mi. No topo da rampa, o skatista parte do repouso (v_inicial = 0 m/s), então sua energia cinética inicial é nula e sua energia mecânica inicial é puramente potencial gravitacional.

E_mi = E_{potencial, inicial} = m . g . h

E_mi = 60 . 10 . 3,0

E_mi = 1800 J

Agora vamos calcular a Energia Mecânica Final E_mf. Na base da rampa temos h = 0, a energia potencial gravitacional é nula e a energia mecânica final é puramente cinética.

E_mf = E_{cinética, final} = (1/2) . m . v²

E_mf = (1/2) . 60 . (6,0)²

E_mf = 30 . 36

E_mf = 1080 J

Vamos então determinar o Trabalho das Forças Dissipativas, W_at. O trabalho das forças dissipativas representa a "perda" de energia mecânica do sistema.

W_at = E_mf - E_mi

W_at = 1080 - 1800

W_at = - 720 J

A questão pede o módulo do trabalho, que é o valor absoluto. Então:|W_at| = 720 J

Resposta correta: alternativa b) V, V, F

Análise da frase I: Se a velocidade é constante, a força resultante é nula. A força motriz (F_motor) deve equilibrar as forças que se opõem ao movimento: a componente do peso paralela à pista (Pₓ) e as forças de resistência (F_res).

Equação de equilíbrio: F_motor = Pₓ + F_res

O peso P é dado por: P = m . g = 10000 . 10 = 100000 N

Para calcular Pₓ devemos usar a equação:

Pₓ = P . sen(θ)

O seno do ângulo (θ) é a razão entre o cateto oposto (altura) e a hipotenusa (distância percorrida). Nesse caso temos sen(θ) = altura / distância = 4 / 100 = 0,04. Assim:

Pₓ = 100000 . 0,04 = 4000 N

Podemos agora calcular a Força Motriz, pois:

F_motor = Pₓ + F_res = 4000 + 5000 = 9000 N

Conclusão: A afirmação está correta.

Análise da frase II: Em um plano inclinado, a força peso (P) é decomposta em duas componentes: Pₓ (paralela ao plano) e Pᵧ (perpendicular ao plano). A força normal (N) é a reação da superfície à componente Pᵧ.

Assim, a força normal (N) equilibra apenas a componente perpendicular do peso (Pᵧ). Matematicamente, temos:

N = Pᵧ = P . cos(θ)

Como o ângulo θ é maior que zero, o valor de cos(θ) será sempre menor que 1. Portanto, a força normal (N) é sempre menor que o peso total (P) em um plano inclinado. A afirmação está correta.

Análise da frase III: Esta afirmação compara o trabalho realizado em duas situações para atingir a mesma altura: subindo a rampa e sendo içado verticalmente.

Trabalho da Força Peso: O trabalho realizado contra a força peso depende apenas da variação da altura pois W_contra,peso = m . g . h.

Este valor é o mesmo para a rampa e para o içamento vertical, pois a altura final é a mesma. Para h = 4m, W_contra,peso = 10000 . 10 . 4 m = 400000 J

Trabalho Total da Força Motriz:

Na rampa: o motor precisa vencer a força peso (componente Pₓ) e a força de resistência. O trabalho total do motor é:

W_motor = F_motor . distância = 9000 . 100 = 900000 J

No içamento vertical (ideal e sem atrito): a força para içar seria igual ao peso de 100000 N. O trabalho seria W_içamento = Força . altura = 100000 . 4 m = 400000 J

Conclusão: O trabalho realizado pelo motor na rampa (900000 J) é maior que o trabalho para um içamento vertical ideal (400000 J), pois na rampa há um trabalho adicional para vencer as forças de resistência ao longo de uma distância maior.

A rampa reduz a força necessária, mas aumenta a distância, e o trabalho contra o atrito torna o trabalho total maior. Portanto, a afirmação de que o trabalho diminui é falsa.

Resposta correta: alternativa d) V, V, V

Análise da frase I: Para encontrar a aceleração, aplicamos a Segunda Lei de Newton Fᵣ = m . a. A força resultante na direção do movimento é a diferença entre a componente do peso que puxa para baixo (Pₓ) e a força de atrito (Fₐₜ).

Equação da força resultante: Fᵣ = Pₓ - Fₐₜ = m . a

Vamos calcular o peso e seu componente na direção do movimento, P_x:

Peso P = m . g = 30 . 10 = 300 N

Pₓ é dado por P × sen(θ)

O seno do ângulo (θ) pode ser obtido pela geometria do escorregador:

sen(θ) = cateto oposto / hipotenusa = altura / comprimento

sen(θ) = 3,0 / 5,0 = 0,6.

Pₓ = 300 . 0,6 = 180 N

Podemos agora calcular a Força Resultante: Fᵣ = Pₓ - Fₐₜ = 180 - 24 = 156 N

Tenso a força resultante podemos achar a aceleração, pois:

a = Fᵣ / m = 156 / 30 = 5,2 m/s²

Conclusão: A afirmação está correta.

Análise da frase II: a aceleração é dada pela fórmula a = (Pₓ - Fₐₜ) / m. Vamos analisar como cada termo se comporta com o aumento do ângulo (θ).

Pₓ = P . sen(θ): à medida que o ângulo θ aumenta e a rampa fica mais íngreme, o valor de sen(θ) também aumenta. Portanto, a força que puxa para baixo (Pₓ) aumenta.

Fₐₜ = μ . N = μ . P . cos(θ): à medida que o ângulo θ aumenta, o valor de cos(θ) diminui. Isso significa que a força normal (N) diminui, e consequentemente, a força de atrito (Fₐₜ) também diminui.

Em um tobogã mais íngreme, a força que acelera (Pₓ) aumenta e a força que freia (Fₐₜ) diminui. Ambos os efeitos contribuem para um aumento da força resultante e, consequentemente, da aceleração.

Conclusão: A afirmação está correta.

Análise da frase III: se o atrito é desprezível, o sistema é conservativo. Isso significa que a energia mecânica no início ou topo do escorregador é igual à energia mecânica no final ou base.

Equação de Conservação da Energia:

E_{mecânica,inicial} = E_{mecânica,final}

Cálculo da energia mecânica Inicial: No topo, a criança parte do repouso e temos E_{cinética, inicial} = 0. Assim, a energia é puramente potencial gravitacional ou E_{mecânica,inicial} = m . g . h

Cálculo da energia mecânica final: Na base, a altura é zero e E_{final,potencial} = 0. Assim, a energia final é puramente cinética: E_{mecânica,final} = (1/2) . m . v²

Igualando as energias, temos:

m . g . h = (1/2) . m . v²

A massa (m) pode ser cancelada em ambos os lados: g . h = (1/2) . v²

A velocidade final é dada por:

Conclusão: A fórmula da velocidade final (v) depende apenas da aceleração da gravidade (g) e da altura vertical (h). O comprimento da rampa não entra na equação. Portanto, a afirmação está correta.