Exercícios sobre função linear (com gabarito explicado)
A função linear é um dos conceitos mais importantes da Matemática no ensino médio e aparece com frequência em vestibulares e no ENEM. Para ajudar você a praticar e fixar o conteúdo, preparamos uma lista de exercícios resolvidos, com gabarito explicado, que exploram diferentes situações do dia a dia em que a função linear pode ser aplicada.
Questão 1
Duas novas empresas de transporte por aplicativo estão começando a atuar em uma certa cidade e para conseguir o máximo de clientes ambas estão fazendo a seguinte promoção:
- Empresa SlowDrive: Cobra um taxa fixa de R$ 5,00 e um adicional de R$ 0,80 por qilômetro rodado.
- Empresa SmoothTrip: Cobra uma taxa fixa de R$ 8,00 e um adicional de R$ 0,70 por quilômetro rodado.
Considerano estas informações e que os crescimentos dos valores a serem pagos em uma corrida são lineares, determine para qual quilometragem a empresa SmoothTrip é a mais vantajosa para o cliente.
a) até 12 km
b) a partir de 20 km
c) até 25 km
d) a partir de 30 km
Inicialmente vamos modelar as funções para as duas empresas
SlowDrive: SD(x) = 5,00 + 0,80x
SmoothTrip: ST(x) = 8,00 + 0,70x
Em seguida, o que queremos é que a SmoothTrip seja mais vantajosa, ou seja, tenha o menor custo o que ocorre se:
ST(x) < SD(x)
8,00 + 0,70x < 5,00 + 0,80x
8,00 - 5,00 < 0,80x - 0,70x
3,00 < 0,10x
0,10x > 3,00
x > 30
Isto é, a SmoothTrip é mais vantajosa para uma viagem a partir de 30 km.
Questão 2
A produção de uma indústria automobilistica vem reduzindo de forma linear ao longo dos anos como mostra o gráfico abaixo:
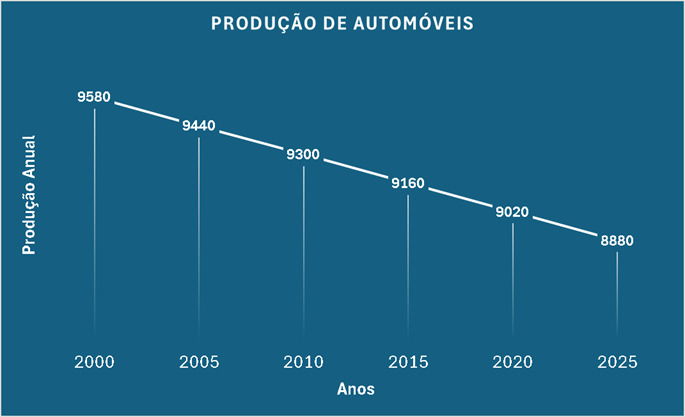
Caso a taxa de variação permaneça constante, qual será a produção dessa indústria em 2047?
a) 8264
b) 9524
c) 8424
d) 8880
Observe que o decréscimo é linear e para cada intervalo de 5 anos a produção reduz 140, ou seja, para cada ano a produção reduz 140/5 = 28.
De 2025 até 2047 são 22 anos tal que a redução será 22 x 28 = 616.
Logo, em 2047 a produção será de 8880 - 616 = 8264.
Questão 3
Considere o gráfico das funções cuja taxa de variação é linear e constante:
e
.
A área do triângulo delimitado pelas funções ,
e o eixo das abscissas vale em unidades de área:
a)
b)
c)
d)
Precisamos determinar os vértices do triângulo que serão obtidos pelos zeros das funções e pela interseção entre elas.
Zero da função
Zero da função
Como a função é linear o zero da função é a origem em
.
Interseção entre e
Portanto, para calcularmos a área de um triângulo precisamos da base e da altura, informações que já obtivemos:
Questão 4
O gráfico abaixo representa uma reta.
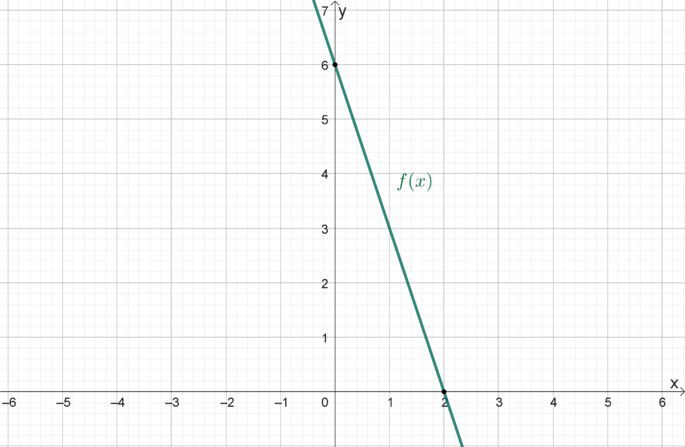
Marque a alternativa que apresenta corretamente a função apresentada no gráfico.
a)
b)
c)
d)
Observe que a reta que representa a função passa por dois pontos e
, como toda função afim
intercepta o eixo
no ponto
temos que
.
Já o coeficiente angular ou taxa de variação é dado por:
Portanto,
Questão 5
Em um exercício de treinamento da marinha mercante duas embarcações Inafundável II e Rota Certa I partem, em linha reta, respectivamente, das seguintes coordenadas cartesianas e
com destinos, respectivamente, em
e
. O objetivo do exercício é identificar as coordenadas de uma possível colisão entre as embarcações. Qual das alternativas abaixo apresenta a possível coordenada de colisão?
a)
b)
c)
d)
Inicialmente devemos obter as funções afim que determinam as trajetórias das embarcações que são da forma
Infundável II:
Rota Certa I:
Agora para identificar as coordenadas de uma possível colisão basta igualarmos as duas funções e resolver a equação resultante:
portanto, as coordenadas de uma possível colisão são
Questão 6
A reta intercepta o eixo
em
e o eixo
em
. Qual o comprimento do segmento
?
a)
b)
c)
d)
Dada a função , temos qua a mesma intercepta o eixo
em
e calculando o zero da função teremos:
O que com a origem forma um triângulo retângulo de catetos e
.
Aplicando o teorema de Pitágoras:
Questão 7
Um reservatório está sendo enchido por uma bomba tal que o volume em litros é dado em função do tempo
em minutos de forma linear. Sabe-se que em
o reservatório encontra-se com
, e em
tinha
. Como a capacidade total do reservatório é de
, em quantos minutos estará completamente cheio?
a) 47 min
b) 53 min
c) 59 min
d) 61 min
De acordo com os dados do problema temos:
Mas como queremos :
Questão 8
Qual deve ser o valor de para que a função definida por
seja decrescente?
a)
b)
c)
d)
Para que a função afim seja decrescente devemos ter
.
Continue praticando com exercícios de Função Afim (Função do 1º Grau): com respostas explicadas.
Referências Bibliográficas
BONJORNO, José Roberto et al. Prisma Matemática: Conjuntos e funções – Ensino Médio. São Paulo: FTD, 2020.
IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David. Fundamentos de Matemática Elementar. Vol. 1: Conjuntos e funções. São Paulo: Atual, 2013.
ILACQUA, Angélica. Funções afim, quadrática, exponencial e logarítmica. São Paulo: Edocente, 2021.
SOUZA, Joamir Roberto de. Multiversos Matemática: Conjuntos e função afim – Ensino Médio. São Paulo: FTD, 2020.
TEIXEIRA, Lilian Aparecida. Superação Matemática – 9º ano. São Paulo: Moderna, 2021.
Exercícios sobre função linear (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-funcao-linear-com-gabarito-explicado/. Acesso em:

