Acelere seu aprendizado

Estudo das derivadas: introdução e regras gerais

Imagine que você está dirigindo em uma estrada e quer saber sua velocidade exata em um momento específico, como no terceiro minuto da viagem.

Se você calcular apenas a distância total percorrida e dividir pelo tempo total, vai encontrar a velocidade média.

Mas isso não mostra a velocidade exata naquele instante. Para entender melhor, vamos transformar essa ideia em uma função matemática.

Pense na distância percorrida (em quilômetros) como algo que depende do tempo (em horas), e essa relação pode ser expressa assim:

$s parêntese esquerdo t parêntese direito igual a t ao quadrado mais 2 t$

onde $t$ representa o tempo em horas e $s parêntese esquerdo t parêntese direito$ a distância em quilômetros.

Agora vem a pergunta "qual é a sua velocidade exatamente no instante em que $t igual a 1$ hora?"

Se calculássemos a velocidade média entre $t igual a 1$ e $t igual a 1 vírgula 1$ , por exemplo, faríamos:

$v igual a numerador incremento s sobre denominador incremento t fim da fração igual a numerador s parêntese esquerdo 1 vírgula 1 parêntese direito menos s parêntese esquerdo 1 parêntese direito sobre denominador 1 vírgula 1 menos 1 fim da fração$

Esse cálculo representa a variação da distância dividida pela variação do tempo, ou seja, a velocidade média nesse intervalo pequeno de tempo.

Quanto menor for o intervalo de tempo, tendendo a zero ou se aproximando de zero, mais nos aproximamos da velocidade instantânea. Ela nada mais é do que a derivada da função naquele ponto.

De forma geral, a derivada serve exatamente para isso: calcular a taxa de variação instantânea de uma função em um determinado ponto.

Neste conteúdo você encontra:

Interpretação geométrica da derivada
Definição de derivada
Notações para derivada
Regras de derivação
Exemplos

Interpretação geométrica da derivada

A derivada representa a inclinação da reta tangente à curva da função em um ponto.
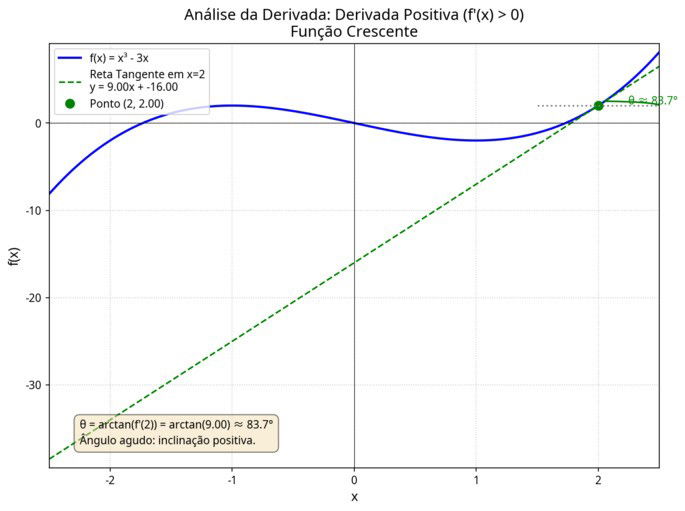
Se a reta está inclinada para cima, a taxa de variação é positiva, indicando que a função está crescendo.
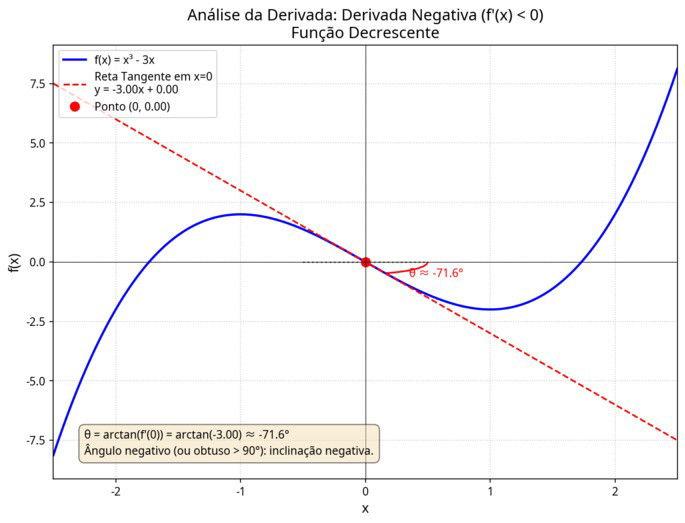
Se a reta está inclinada para baixo, a taxa de variação é negativa, mostrando que a função está diminuindo.
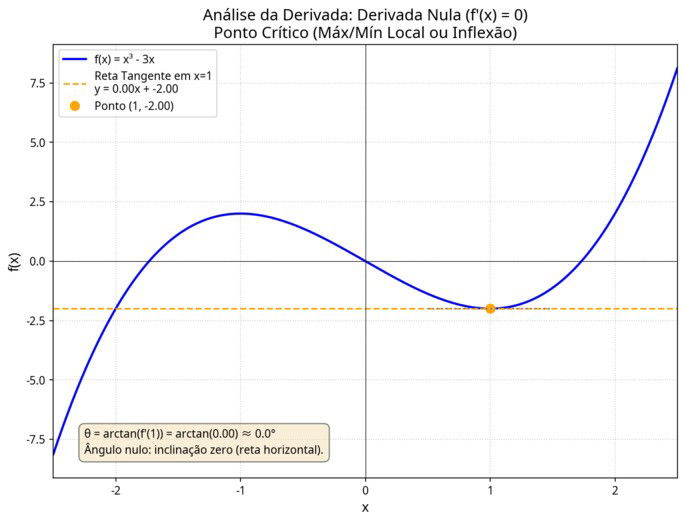
Se a reta é horizontal, a taxa de variação é zero. Nesse caso, a função não cresce nem diminui naquele ponto.

Derivada positiva

Derivada nula

Remover anúncios

Derivada negativa

A derivada é um conceito que surge a partir do limite e serve para calcular, com precisão, como uma função varia em um ponto específico. Ela indica a taxa de crescimento ou decrescimento da função naquele instante.

Definição de derivada

É dada pela taxa de variação instantânea de uma determinada função.

$f apóstrofo parêntese esquerdo x parêntese direito igual a limite como h seta para a direita 0 de numerador f parêntese esquerdo x mais h parêntese direito menos f parêntese esquerdo x parêntese direito sobre denominador h fim da fração$

Nosso objetivo é encontrar a velocidade instantânea, que é a derivada da função posição:

$s parêntese esquerdo t parêntese direito igual a t ao quadrado mais 2 t$

Aplicando a definição na função:

$s apóstrofo parêntese esquerdo t parêntese direito igual a limite como h seta para a direita 0 de numerador s parêntese esquerdo t mais h parêntese direito menos s parêntese esquerdo t parêntese direito sobre denominador h fim da fração s apóstrofo parêntese esquerdo t parêntese direito igual a limite como h seta para a direita 0 de numerador parêntese esquerdo t mais h parêntese direito ao quadrado mais 2 parêntese esquerdo t mais h parêntese direito menos t ao quadrado menos 2 t sobre denominador h fim da fração s apóstrofo parêntese esquerdo t parêntese direito igual a limite como h seta para a direita 0 de numerador t ao quadrado mais 2 t h mais h ao quadrado mais 2 t mais 2 h menos t ao quadrado menos 2 t sobre denominador h fim da fração s apóstrofo parêntese esquerdo t parêntese direito igual a limite como h seta para a direita 0 de numerador h parêntese esquerdo h mais 2 t mais 2 parêntese direito sobre denominador h fim da fração s apóstrofo parêntese esquerdo t parêntese direito igual a limite como h seta para a direita 0 de parêntese esquerdo h mais 2 t mais 2 parêntese direito s apóstrofo parêntese esquerdo t parêntese direito igual a 2 t mais 2$

A função derivada $s apóstrofo parêntese esquerdo t parêntese direito igual a 2 t mais 2$ representa a velocidade instantânea em qualquer instante $t$ .

Em nosso caso, no instante $t igual a 1$ , a velocidade é:

$s apóstrofo parêntese esquerdo 1 parêntese direito igual a 2 sinal de multiplicação 1 mais 2 igual a 4 espaço k m dividido por h$

Ou seja, exatamente nesse momento, o carro está a 4 km/h.

Notações para derivada

A derivada de uma função pode ser representada de diferentes maneiras. Todas essas notações possuem o mesmo significado, mas são utilizadas em contextos distintos, de acordo com a área de estudo, o autor ou até a preferência de quem escreve.

Notação de Leibniz

É uma das mais conhecidas e muito usada na Física, na Engenharia e em aplicações práticas.

Seja uma função $y igual a f parêntese esquerdo x parêntese direito$ , a derivada de $y$ em relação a $x$ é representada por:

$numerador d y sobre denominador d x fim da fração$

Lê-se: "derivada de $y$ em relação a $x$ ".

Se quisermos indicar a derivada calculada em um ponto específico, podemos escrever, por exemplo:

$numerador d y sobre denominador d x fim da fração em moldura direita fecha moldura com x igual a a subscrito fim do subscrito$

Que significa a derivada de $y$ em relação a $x$ quando $x$ é igual a $a$ .

Notação de Lagrange

Muito utilizada no ensino médio e superior, especialmente em livros de Cálculo.

Remover anúncios

Seja uma função $f parêntese esquerdo x parêntese direito$ , sua derivada é indicada por:

$f apóstrofo parêntese esquerdo x parêntese direito$

Lê-se: " $f$ linha de $x$ ".

Se for uma função chamada $y igual a f parêntese esquerdo x parêntese direito$ , também podemos escrever:

$y apóstrofo$

Notação de Newton

Muito comum na Física, especialmente quando a variável independente é o tempo.

A derivada de uma função em relação ao tempo é representada por um ponto sobre a variável:

$y com ponto sobrescrito$

Lê-se: " $y$ ponto".

Notação de Euler (D operador)

Usada em contextos mais formais, principalmente em Equações Diferenciais.

Seja uma função $y igual a f parêntese esquerdo x parêntese direito$ , sua derivada pode ser representada como:

$D abre colchetes y fecha colchetes$ ou $D f parêntese esquerdo x parêntese direito$

Ou seja, o operador D aplicado à função.

Regras de derivação

Para não precisarmos recorrer ao limite toda vez temos técnicas que tornam esse cálculo muito mais prático. São as chamadas regras de derivação como da potência, produto, quociente e da composição de funções, esta última conhecida como regra da cadeia.

Derivada de uma constante

A derivada de uma constante é sempre igual a zero.

$y igual a k seta dupla para a direita y apóstrofo igual a 0$

Regra da potência

É aplicada quando a função está elevada a uma potência.

$y igual a x à potência de n seta dupla para a direita y apóstrofo igual a n. x à potência de n menos 1 fim do exponencial$

Regra do produto

Quando temos o produto de duas ou mais funções.

$y igual a u. v seta dupla para a direita y apóstrofo igual a u apóstrofo. v mais u. v apóstrofo$

Regra do quociente

Quando temos o quociente entre funções.

$y igual a u sobre v seta dupla para a direita y apóstrofo igual a numerador u apóstrofo. v menos u. v apóstrofo sobre denominador v ao quadrado fim da fração$

Regra da cadeia (função composta)

É a regra de derivação para funções compostas.

$y apóstrofo igual a f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito seta dupla para a direita y apóstrofo igual a f apóstrofo parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito. g apóstrofo parêntese esquerdo x parêntese direito$

$numerador d y sobre denominador d x fim da fração igual a numerador d y sobre denominador d u fim da fração sinal de multiplicação numerador d u sobre denominador d x fim da fração$

A regra da cadeia é uma ferramenta poderosa que nos permite derivar funções complexas construídas a partir de funções mais simples.

Derivadas de funções trigonométricas

As principais funções trigonométricas são seno, cosseno e tangente e suas derivadas são:

$y igual a s e n parêntese esquerdo x parêntese direito seta dupla para a direita y apóstrofo igual a cos parêntese esquerdo x parêntese direito y igual a cos parêntese esquerdo x parêntese direito seta dupla para a direita y apóstrofo igual a menos s e n parêntese esquerdo x parêntese direito y igual a tan parêntese esquerdo x parêntese direito seta dupla para a direita y apóstrofo igual a s e c ao quadrado parêntese esquerdo x parêntese direito$

Derivadas de funções exponenciais e logarítmicas

Elas modelam crescimento/decrescimento (população, juros, radioatividade) e são essenciais em equações diferenciais, probabilidade e machine learning.

$y igual a e à potência de x seta dupla para a direita y apóstrofo igual a e à potência de x y igual a a à potência de x seta dupla para a direita y apóstrofo igual a a à potência de x. ln parêntese esquerdo a parêntese direito y igual a ln parêntese esquerdo x parêntese direito seta dupla para a direita y apóstrofo igual a 1 sobre x y igual a log com a subscrito espaço x seta dupla para a direita y apóstrofo igual a numerador 1 sobre denominador x. ln parêntese esquerdo a parêntese direito fim da fração$

A derivada representa, de forma simples, a taxa de variação instantânea de uma função em relação a uma de suas variáveis. Geometricamente, ela indica a inclinação da reta tangente à curva em um ponto específico.

Se a derivada é positiva, a função está crescendo. Se é negativa, está decrescendo. Já uma derivada nula aponta um ponto crítico, que pode ser um máximo, um mínimo local ou um ponto de inflexão, sempre com tangente horizontal.

As regras de derivação, embora exijam prática, tornam o processo de cálculo muito mais eficiente. Elas se aplicam a funções simples e também a expressões mais complexas, como produtos, quocientes e composições.

Remover anúncios

Exemplo 1

Considere a função $f parêntese esquerdo x parêntese direito igual a numerador x ao quadrado menos 10 sobre denominador x fim da fração$ . Qual a equação da reta tangente ao gráfico de $f parêntese esquerdo x parêntese direito$ no ponto de abscissa $x igual a 4$ ?

Solução:

A equação da reta tangente ao gráfico da função tem coeficiente angular igual ao valor da derivada da função no ponto $x igual a 4$ .

Observe que a função a ser derivada apresenta quociente, potência e constante.

Primeiro derivamos a função no numerador aplicando a derivada da potencia e a derivada da constante.

$u igual a x ao quadrado menos 10 u apóstrofo igual a 2 x$

Em seguida derivamos o denominador aplicando a derivada da potência.

$v igual a x v apóstrofo igual a 1$

Agora aplicamos a regra do quociente.

$f parêntese esquerdo x parêntese direito igual a u sobre v seta dupla para a direita f apóstrofo parêntese esquerdo x parêntese direito igual a numerador u apóstrofo. v menos u. v apóstrofo sobre denominador v ao quadrado fim da fração$

Substituímos as informações obtidas.

$f apóstrofo parêntese esquerdo x parêntese direito igual a numerador u apóstrofo. v menos u. v apóstrofo sobre denominador v ao quadrado fim da fração f apóstrofo parêntese esquerdo x parêntese direito igual a numerador 2 x. x menos parêntese esquerdo x ao quadrado menos 10 parêntese direito.1 sobre denominador x ao quadrado fim da fração f apóstrofo parêntese esquerdo x parêntese direito igual a numerador 2 x ao quadrado menos x ao quadrado mais 10 sobre denominador x ao quadrado fim da fração f apóstrofo parêntese esquerdo x parêntese direito igual a numerador x ao quadrado mais 10 sobre denominador x ao quadrado fim da fração$

Para obter a equação da reta tangente no ponto de abscissa $4$ , vamos precisar a ordenada desse ponto e basta substituir $x igual a 4$ na função original.

$f parêntese esquerdo x parêntese direito igual a numerador x ao quadrado menos 10 sobre denominador x fim da fração f parêntese esquerdo 4 parêntese direito igual a numerador 4 ao quadrado menos 10 sobre denominador 4 fim da fração f parêntese esquerdo 4 parêntese direito igual a numerador 16 menos 10 sobre denominador 4 fim da fração f parêntese esquerdo 4 parêntese direito igual a 6 sobre 4 f parêntese esquerdo 4 parêntese direito igual a 3 sobre 2$

Logo, o ponto de tangencia é $abre parênteses 4 vírgula 3 sobre 2 fecha parênteses$ .

A equação da reta tangente tem a forma:

$y igual a a x mais b a igual a f apóstrofo parêntese esquerdo 4 parêntese direito igual a numerador 4 ao quadrado mais 10 sobre denominador 4 ao quadrado fim da fração igual a 26 sobre 16 igual a 13 sobre 8$

Agora substituímos o ponto e o coeficiente angular para determinar o coeficiente linear da reta tangente.

$y igual a a x mais b 3 sobre 2 igual a 13 sobre 8 sinal de multiplicação 4 mais b 3 sobre 2 igual a 13 sobre 2 mais b 3 sobre 2 menos 13 sobre 2 igual a b menos 10 sobre 2 igual a b b igual a menos 5$

Por fim temos a equação da reta tangente a curva da função $f$ no ponto $x igual a 4$ .

$y igual a 13 sobre 8 x menos 5$

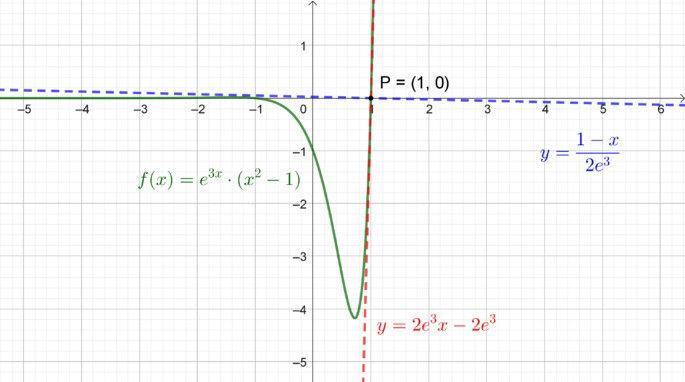
O gráfico a seguir apresenta a função e sua reta tangente no ponto especificado.

Remover anúncios

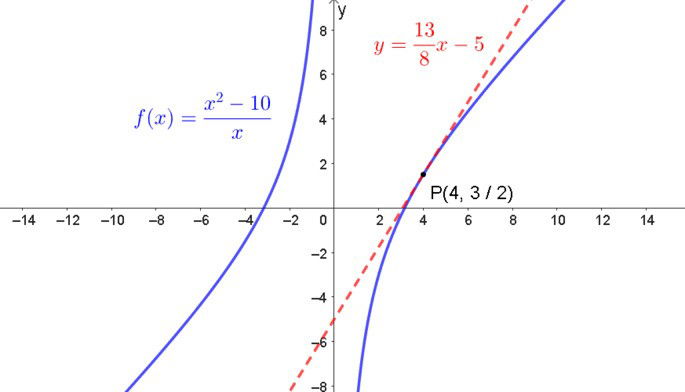
Exemplo 2

Determinar a derivada da função $f parêntese esquerdo x parêntese direito igual a abre parênteses x ao quadrado menos 3 x mais 10 fecha parênteses sinal de multiplicação cos abre parênteses x fecha parênteses$ .

A função apresentada é formada pelo produto de uma função polinomial com uma função trigonométrica. Para calcular sua derivada, devemos aplicar a regra do produto, além de utilizar as derivadas da função potência e da função trigonométrica envolvida.

A derivada do produto é dada pela regra:

$f abre parênteses x fecha parênteses igual a u. v seta dupla para a direita f apóstrofo abre parênteses x fecha parênteses igual a u apóstrofo. v mais u. v apóstrofo$

Chamando de $u igual a x ao quadrado menos 3 x mais 10$ e $v igual a cos abre parênteses x fecha parênteses$ calculamos as suas respectivas derivadas.

Para $u$ aplicamos a regra da potência e a derivada da constante.

$u igual a x ao quadrado menos 3 x mais 10 u apóstrofo igual a 2 x menos 3$

Para $v$ usamos a derivada da função cosseno.

$v igual a cos abre parênteses x fecha parênteses v apóstrofo igual a menos s e n abre parênteses x fecha parênteses$

Por fim, aplicamos a regra do produto e simplificamos se possível.

$f apóstrofo abre parênteses x fecha parênteses igual a u apóstrofo. v mais u. v apóstrofo f apóstrofo abre parênteses x fecha parênteses igual a abre parênteses 2 x menos 3 fecha parênteses. cos abre parênteses x fecha parênteses mais abre parênteses x ao quadrado menos 3 x mais 10 fecha parênteses. abre parênteses menos s e n abre parênteses x fecha parênteses fecha parênteses f apóstrofo abre parênteses x fecha parênteses igual a abre parênteses 2 x menos 3 fecha parênteses. cos abre parênteses x fecha parênteses menos abre parênteses x ao quadrado menos 3 x mais 10 fecha parênteses. s e n abre parênteses x fecha parênteses$

Exemplo 3

Determinar a derivada da função $g abre parênteses x fecha parênteses igual a x ao cubo. tan abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses$ .

Neste caso podemos perceber que a função dada é o produto entre uma função polinomial e uma trigonométrica, sendo a trigonométrica composta com outra polinomial.

Para calcular a derivada da função vamos precisar derivar a potência, a tangente e aplicar as regras do produto e da cadeia para funções compostas.

$g parêntese esquerdo x parêntese direito igual a u. v seta dupla para a direita g apóstrofo abre parênteses x fecha parênteses igual a u apóstrofo. v mais u. v apóstrofo$

Fazendo, $u igual a x ao cubo$ encontramos a sua derivada aplicando diretamente a derivada da potência.

$u igual a x ao cubo u apóstrofo igual a 3 x ao quadrado$

Agora, para derivar a função $v igual a tan abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses$ , vamos aplicar a regra da cadeia. Primeiro, derivamos a função "de fora", neste caso, a tangente e depois multiplicamos esse resultado pela derivada da função "de dentro", que é a função polinomial.

$v igual a tan abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses v apóstrofo igual a s e c ao quadrado abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses. abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses apóstrofo v apóstrofo igual a s e c ao quadrado abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses. abre parênteses 3 x ao quadrado menos 8 x mais 7 fecha parênteses$

Por fim, utilizamos a regra do produto.

$g apóstrofo abre parênteses x fecha parênteses igual a u apóstrofo. v mais u. v apóstrofo g apóstrofo abre parênteses x fecha parênteses igual a 3 x ao quadrado. tan abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses mais x ao cubo. s e c ao quadrado abre parênteses x ao cubo menos 4 x ao quadrado mais 7 x menos 8 fecha parênteses. abre parênteses 3 x ao quadrado menos 8 x mais 7 fecha parênteses$

Exemplo 4

Dada a função $f abre parênteses x fecha parênteses igual a e à potência de 3 x fim do exponencial. abre parênteses x ao quadrado menos 1 fecha parênteses$ obtenha as equações da reta tangente e da reta normal a curva da função no ponto $abre parênteses 1 vírgula 0 fecha parênteses$ .

Sabemos da geometria analítica que as retas tangente e normal são perpendiculares entre si, logo o produto de seus coeficientes angulares vale $a com tan g e n t e subscrito fim do subscrito. a com n o r m a l subscrito fim do subscrito igual a menos 1$ .

A derivada de uma função, quando calculada em um ponto específico, indica o coeficiente angular da reta tangente ao gráfico nesse ponto.

No caso desta função devemos aplicar a regra do produto para encontrar sua derivada.

$f abre parênteses x fecha parênteses igual a u. v seta dupla para a direita f apóstrofo abre parênteses x fecha parênteses igual a u apóstrofo. v mais u. v apóstrofo u igual a e à potência de 3 x fim do exponencial u apóstrofo igual a e à potência de 3 x fim do exponencial. abre parênteses 3 x fecha parênteses apóstrofo espaço parêntese esquerdo r e g r a espaço d a espaço c a d e i a parêntese direito u apóstrofo igual a e à potência de 3 x fim do exponencial.3 u apóstrofo igual a 3 e à potência de 3 x fim do exponencial v igual a x ao quadrado menos 1 v apóstrofo igual a 2 x f apóstrofo abre parênteses x fecha parênteses igual a 3 e à potência de 3 x fim do exponencial. abre parênteses x ao quadrado menos 1 fecha parênteses mais e à potência de 3 x fim do exponencial.2 x$

Agora calculamos o coeficiente angular da reta tangente no ponto $abre parênteses 1 vírgula 0 fecha parênteses$ .

$f apóstrofo abre parênteses x fecha parênteses igual a 3 e à potência de 3 x fim do exponencial. abre parênteses x ao quadrado menos 1 fecha parênteses mais e à potência de 3 x fim do exponencial.2 x a com tan g e n t e subscrito fim do subscrito igual a f apóstrofo abre parênteses 1 fecha parênteses igual a 3 e à potência de 3.1 fim do exponencial. abre parênteses 1 ao quadrado menos 1 fecha parênteses mais e à potência de 3.1 fim do exponencial.2.1 a com tan g e n t e subscrito fim do subscrito igual a 2 e ao cubo$

Substituindo o ponto na equação da reta encontraremos o coeficiente linear.

$y igual a a x mais b 0 igual a 2 e ao cubo.1 mais b b igual a menos 2 e ao cubo$

E portanto, a equação da reta tangente é:

$y igual a 2 e ao cubo x menos 2 e ao cubo$

Para reta normal teremos o seguinte coeficiente:

$a com tan g e n t e subscrito fim do subscrito. a com n o r m a l subscrito fim do subscrito igual a menos 1 2 e ao cubo. a com n o r m a l subscrito fim do subscrito igual a menos 1 a com n o r m a l subscrito fim do subscrito igual a menos numerador 1 sobre denominador 2 e ao cubo fim da fração$

Substituímos na equação da reta.

$y igual a m x mais n 0 igual a menos numerador 1 sobre denominador 2 e ao cubo fim da fração.1 mais n n igual a numerador 1 sobre denominador 2 e ao cubo fim da fração$

Por fim,

$y igual a menos numerador 1 sobre denominador 2 e ao cubo fim da fração x mais numerador 1 sobre denominador 2 e ao cubo fim da fração$ ou $y igual a numerador 1 menos x sobre denominador 2 e ao cubo fim da fração$

Está na hora de praticar com: Exercícios de derivadas (com gabarito respondido e explicado)

Referências Bibliográficas

GUIDORIZZI, Hamilton Luiz. Um Curso de Cálculo. v. 1. 5. ed. Rio de Janeiro: LTC, 2013.

IEZZI, Gelson; MURAKAMI, Carlos; MACHADO, Nilson José. Fundamentos de Matemática Elementar: Limites, Derivadas, Noções de Integral. v. 8. 7. ed. São Paulo: Atual, 2013.

MACHADO, Antonio dos Santos. Matemática: Temas e Metas. v. 6: Funções e Derivadas. São Paulo: Atual, 1988. ISBN 978-8570560520.

MUNEM, Mustafá A.; FOUDBA, David J. Cálculo: Uma abordagem intuitiva e aplicada. v. 1. São Paulo: Pearson, 2009.

STEWART, James. Cálculo. v. 1. 8. ed. São Paulo: Cengage Learning, 2016.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações

Remover anúncios