Equação da continuidade: entenda o que é e a fórmula (com exercícios)
A equação da continuidade descreve o movimento laminar de líquidos em tubos e encanamentos, ou seja, descreve o movimento de um líquido em condições ideais onde não existe atrito entre as partículas do líquido com o tubo e nem entre si. Atente que o atrito em escoamentos causam turbulências.
Em linhas gerais a equação da continuidade diz que, em um sistema fechado que não possui perdas, a quantidade de líquido ou o volume de um fluido que entra no sistema deve ser exatamente igual à quantidade de líquido ou o volume de um fluido que sai do sistema. Ela é expressa como:
Onde:
- A1, A2, A3, ..., An são as áreas das secções transversais pelas alturas, respectivamente, nos pontos 1, 2, 3, ... , n do sistema,
- v1, v2, v3, ..., vn são as velocidades de escoamento do líquidos, respectivamente, nos pontos 1, 2, 3, ... , n do sistema,
- n representa um ponto qualquer do sistema.
Dedução da equação da continuidade
A equação da continuidade é uma consequência direta da conservação da densidade do líquido e da conservação da quantidade de líquido que escoa em um tubo, independente das características do tubo.
Considere um líquido que escoa por um tubo cujas dimensões variam, conforme ilustrado na figura abaixo:
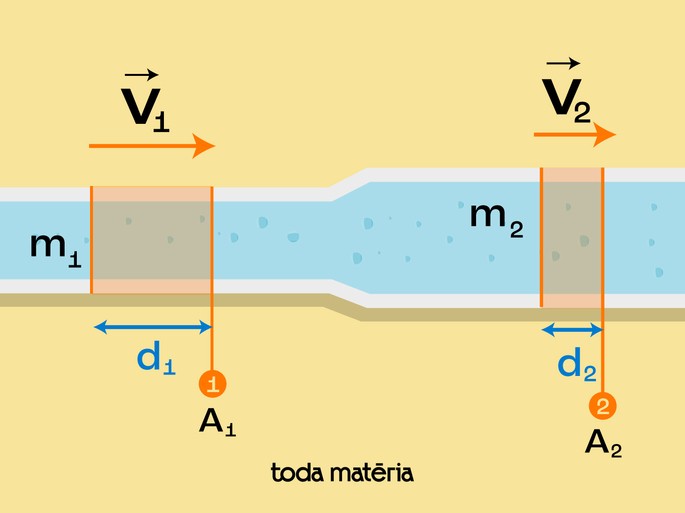
Se o líquido é incompressível, sua densidade não varia durante o escoamento. Ela se mantém constante e imutável independente do estreitamento que ocorre no tubo, ou seja: .
Lembrando que a densidade é dada pela relação da massa pelo volume, e juntando essa informação com a igualdade da densidade em qualquer região do tubo, temos:
O volume de um tubo cilíndrico é dado pela multiplicação da área da secção transversal pela altura, ou V = A.d. Substituindo V1 e V2, respectivamente, por A1.d1 e A2.d2, temos:
A distância percorrida pelo líquido é dada pela multiplicação da velocidade do líquido pelo tempo ou: d = v.t. Substituindo d1=v1.t1 e d2=v2.t2, ficamos com:
Como a condição inicial da equação da continuidade é que o líquido é incompressível, temos que a massa 1 que atravessa uma região 1 do tubo em um tempo 1 é exatamente igual à massa 2 que atravessa uma região 2 no tempo 2. Isso implica em:
Ficamos então com:
Que é a equação da continuidade!
Observe que a velocidade em uma dada região do tubo é inversamente proporcional à área da região, ou:
Assim temos que, quando o tubo fica mais estreito, a velocidade do líquido aumenta. Só assim não ocorre um acúmulo de líquido que fatalmente faria com que a densidade aumentasse.
Definimos ainda a relação entre o volume de líquido que atravessa uma dada região do tempo em um dado tempo como sendo o fluxo do líquido. Ele é representado pela letra e medido em unidade de volume/tempo, podendo ser cm3/s ou l/s.
Exercícios sobre a equação da continuidade
Exercício 1
Quais são as bases da equação da continuidade?
a) A conservação da densidade do líquido e da velocidade de escoamento do líquido.
b) A conservação da velocidade do líquido e da quantidade de líquido que entra e sai do sistema.
c) A conservação da viscosidade do líquido e da quantidade de líquido que entra e sai do sistema.
d) A conservação da densidade do líquido e da quantidade de líquido que entra e sai do sistema.
Resposta correta: alternativa d) A conservação da densidade do líquido e da quantidade de líquido que entra e sai do sistema.
A equação da continuidade é obtida a partir da conservação da densidade do líquido e de que a quantidade de líquido que entra e que sai do sistema é a mesma, ou seja, não há perdas no sistema.
Exercício 2
A água atravessa um tubo de área transversal igual a 10cm2 com velocidade de 50cm/s. Qual será sua velocidade de a área da secção transversal for dividida por dois?
a) 25 cm/s
b) 5 cm/s
c) 100 cm/s
d) 500 cm/s
Resposta correta: alternativa c) 100 cm/s.
Pela equação da continuidade temos que:
A1 . v1 = A2 . v2
Substituindo os valores dados no enunciado, temos:
10 . 50 = 5 . v2
v2 = 100 cm/s
Exercício 3
Qual é a vazão de uma máquina de lavar roupas de 10kg se ela usa 20 litros de água e demora 20 minutos para encher?
a) 0,02 l/s
b) 1 l/s
c) 0,5 l/s
d) 10 l/s
Resposta correta: alternativa a) 0,02 l/s
A vazão é definida como o volume de líquido pela unidade de tempo ou:
Vamos determinar a vazão em litros/segundo.
Exercício 4
Um jardineiro quer regar uma planta que está a 3 metros de distância, mas a mangueira possui apenas 2 metros de comprimento e a água cai no chão a apenas 50 cm da mangueira. Como a equação da continuidade pode ajudá-lo a resolver esse problema?
a) Ele pode abrir mais a saída da água porque assim a água irá mais longe.
b) Ele pode tampar com o dedo parte da saída da água porque assim a água irá cair mais longe.
c) Ele pode tampar com o dedo parte da saída da água porque assim a água irá cair mais perto.
d) Nada do que ele fizer irá fazer com que a água atinja a planta que está a 3 metros de distância.
Resposta correta: alternativa b) Ele pode tampar com o dedo parte da saída da água porque assim a água irá cair mais longe.
A equação da continuidade diz que a velocidade do líquido é inversamente proporcional à área do tubo, ou seja, quanto menor for a saída do tubo, maior será a velocidade da líquido.
O que o jardineiro precisa fazer é diminuir a área de saída da água. Isso fará com que ela saia com maior velocidade da mangueira, podendo atingir a planta que está mais distante.
Continue praticando com mais exercícios sobre a equação da continuidade (com questões resolvidas).
Referências Bibliográficas
Çengel, Y.A.,Cimbala, J.M. Mecânica dos fluidos. AMGH Editora, 1 de fev. de 2015, 3.ed.
Silva, R.F., Santos, E., Cruz, D.F.S. Escoamento de fluidos em tanques: uma ferramenta alternativa para o ensino de Mecânica dos Fluidos. Revista Tecnia. v.2 n.1 2017. Acesso em 12/05/2025.
Equação da continuidade: entenda o que é e a fórmula (com exercícios). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/equacao-da-continuidade-entenda-o-que-e-e-a-formula-com-exercicios/. Acesso em:

