Campo gravitacional: o que é, fórmulas para calcular e exemplos (com exercícios)

Você já reparou que quando deixa cair uma caneta, bola ou xícara da mesa, ela sempre chega ao chão? Ou que a Lua gira em torno da Terra, e a Terra gira em torno do Sol? Esses são exemplos práticos do funcionamento dos campos gravitacionais.

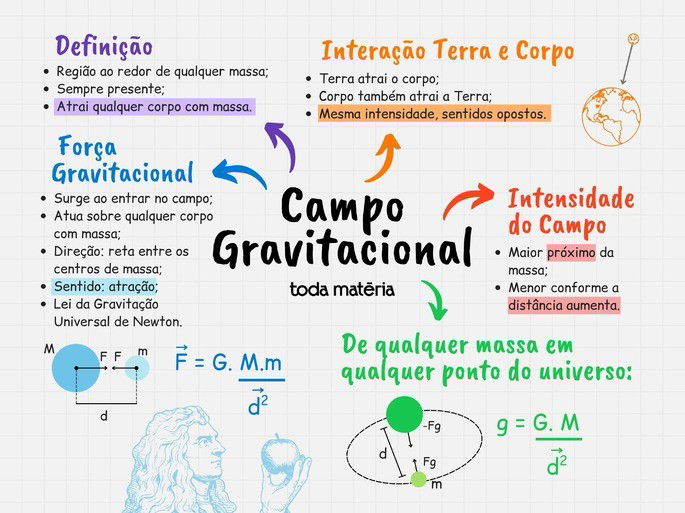
Um campo gravitacional é uma região do espaço em volta de qualquer objeto que tenha massa, onde outros corpos são atraídos. Quanto maior a massa do objeto, mais forte será o seu campo gravitacional.

Por exemplo, o Sol tem um campo gravitacional muito forte, por isso consegue manter planetas orbitando ao seu redor. Já o seu próprio corpo também tem um campo gravitacional, só que ele é muito pequeno. É por isso que você não vê objetos orbitando à sua volta!

Todos os corpos que são colocados na presença de um campo gravitacional, estarão automaticamente sujeitos à uma força gravitacional, sem exceção.

Como surge e funciona o campo gravitacional

Todo corpo que possui massa cria automaticamente um campo gravitacional em torno de si. Esse campo atua atraindo outros objetos com massa. O efeito dessa atração depende principalmente de dois fatores:

Massa dos corpos: quanto maior a massa, mais forte será a atração.

Distância entre os corpos: quanto mais próximos os corpos estiverem, maior será a força gravitacional.

Relação entre campo gravitacional e força gravitacional

A força de atração ou força gravitacional entre um corpo de massa m e outro de massa M é descrita pela Lei da Gravitação Universal de Newton e se dá nos campos gravitacionais dos dois corpos.

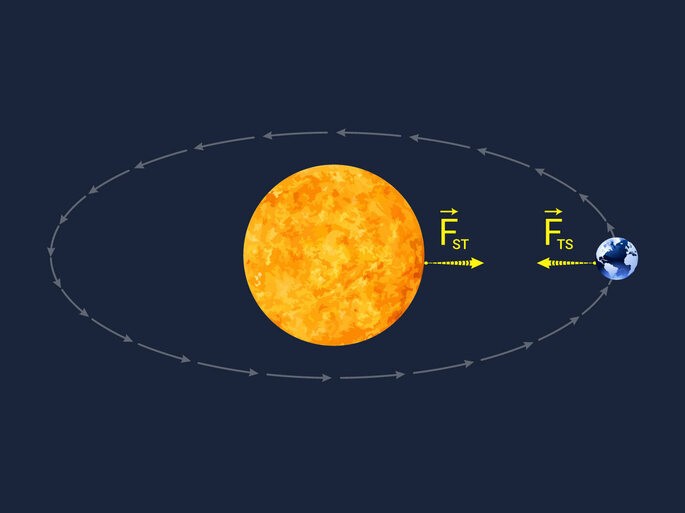
Assim, o Sol possui um campo gravitacional ao seu redor onde atua uma força que atrai a Terra em sua direção. Essa força é proporcional às massas do Sol e da Terra e inversamente proporcional à distância entre eles.

A Terra também possui um campo gravitacional no seu entorno que produz uma força que atrai o Sol. Essa força também é proporcional às massas da Terra e do Sol e inversamente proporcional à distância entre eles.

As duas forças, e , possuem a mesma intensidade e direção, mas sentidos contrários. Uma delas atuando no Sol e a outra na Terra. Essas características mostram que elas funcionam exatamente como um par de forças de Ação e Reação da Terceira Lei de Newton.

Observe a imagem abaixo que mostra o par de Ação e Reação da Força de Atração entre a Terra e o Sol:

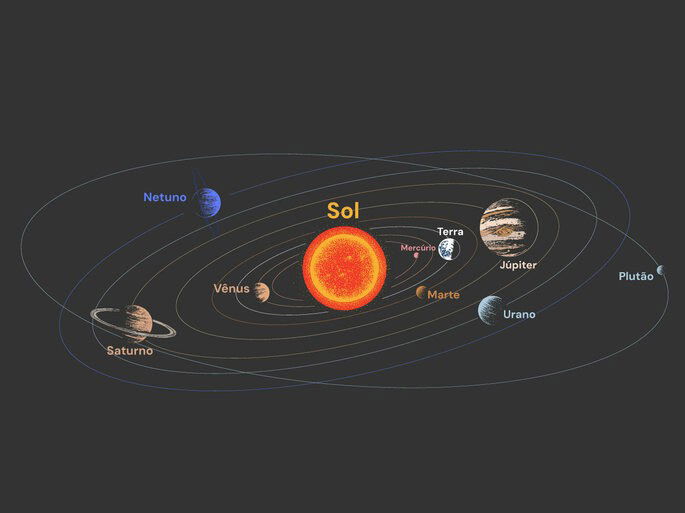
Este mesmo raciocínio pode ser aplicado a cada um dos planetas do nosso Sistema Solar, pois todos eles possuem massa e, portanto, campo gravitacional.

Isso faz com que cada planeta do nosso Sistema Solar seja visto também como um centro atrator, como o Sol. Como centros atratores, cada um dos planetas atrai o Sol e também todos os demais planetas e, pela Lei da Ação e Reação, é também atraído pelo Sol e por cada um dos outros planetas.

Os planetas orbitam em torno do Sol e não ao contrário por conta das relações das massas. Como a massa do Sol é muito maior do que as dos planetas, seu campo gravitacional e sua inércia também são muito maiores e, por esse motivo, ele permanece parado no centro do nosso Sistema Solar.

Mas, os campos gravitacionais dos planetas interferem nos movimentos orbitais, fazendo com que cada um dos planetas percorra uma órbita elíptica própria e não circular em torno do Sol.

Como calcular o campo gravitacional (fórmula)

Para entender como calcular o campo gravitacional, precisamos primeiro entender a força gravitacional descrita pela Lei da Gravitação Universal de Newton:

onde

• é a força gravitacional que existe entre os dois corpos,
• é a distância entre os dois corpos, medida a partir dos centros de massa dos mesmos e,
• G é a constante gravitacional igual em qualquer lugar do universo. Seu valor é 6,67 x 10^-11 N.m²/Kg².

A direção da força gravitacional é a da linha que une os centros de massa dos dois corpos e o sentido é o apontado para o outro corpo.

Para determinar a equação do campo gravitacional de qualquer massa do universo, precisamos começar relembrando a força de atração entre a Terra e um corpo em sua superfície, chamada força peso ou apenas peso.

A força peso de um corpo na superfície da Terra é igual à força de atração entre a Terra e o corpo. O peso é dado por onde m é a massa do corpo e é a aceleração da gravidade ou campo gravitacional da Terra.

Isolando na equação do peso e, explicitando que a aceleração da gravidade ou campo gravitacional nesse caso é o da Terra, temos:

Podemos usar esse mesmo raciocínio para calcular o campo gravitacional de qualquer corpo no universo, a partir da equação da força gravitacional da gravitação universal, ou:

Isolando temos:

Assim obtemos que o campo gravitacional de qualquer massa em qualquer ponto do universo é igual a:

Exemplo resolvido

Qual é o valor do campo gravitacional sentido por uma pessoa de 80 Kg que se encontra na superfície da Terra?

Dados: massa da Terra = 5,9722×10²⁴ kg, raio da Terra = 6.3781×10⁶ m e G = 6,67 x 10^-11 N.m²/Kg²

Resolução:

A equação do módulo do campo gravitacional é

Substituindo os valores temos:

Ou seja, o campo gravitacional sentido por uma pessoa na superfície da Terra é igual ao valor usado na Física para a aceleração da gravidade, ou seja, g = 9,79 m/s².

Resumo do campo e da força gravitacionais

O campo gravitacional é uma área no espaço em torno de qualquer massa que está sempre presente e que atua como um campo de força que atrai qualquer corpo que adentre essa área.

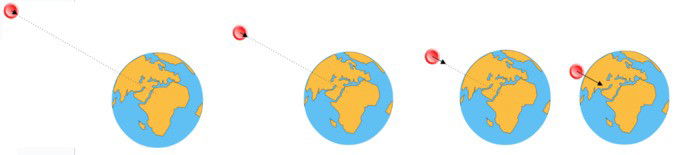
Na figura abaixo o campo gravitacional de uma massa M está representado como círculos brancos e azuis em torno da massa.

Apesar de na representação o campo gravitacional ser representado como sendo plano, ele é na verdade esférico.

Observe que o campo gravitacional é mais intenso (mais branco na figura) nas proximidades da massa e torna-se cada vez mais fraco (ou rarefeito na figura) com o aumento da distância. Isso está em pleno acordo com a equação do campo, a saber:

Um corpo que adentra o campo gravitacional de uma massa automaticamente passa a ser atraído por uma força gravitacional, que age segundo a fórmula:

Abaixo mostramos uma representação da força gravitacional existente entre a Terra e uma esfera em diferentes distâncias ou

Atente que a figura mostra apenas a força de atração da Terra na esfera para não poluir a imagem. Mas lembre que o corpo m também atrai a Terra com uma força de mesma intensidade e direção, mas de sentido contrário.

Aprofunde os seus estudos sobre o assunto:

• Força Gravitacional - Lei da Gravitação Universal
• Gravidade
• Exercícios sobre campo gravitacional (com questões explicadas)
• Exercícios sobre a gravitação universal (com questões resolvidas)