Áreas de Figuras Planas

Rosimar Gouveia

Professora de Matemática e Física

As áreas das figuras planas medem o tamanho da superfície da figura. Desse modo, podemos pensar que quanto maior a superfície da figura, maior será sua área.

Geometria Plana e Espacial

A Geometria plana é a área da matemática que estuda as figuras planas. Ou seja, aquelas que possuem comprimento e largura, sendo figuras bidimensionais (duas dimensões).

O que as difere das figuras geométricas espaciais é que estas apresentam três dimensões e incluem, portanto, o conceito de volume.

Saiba mais:

• Geometria Plana
• Geometria Espacial

Principais Figuras Planas

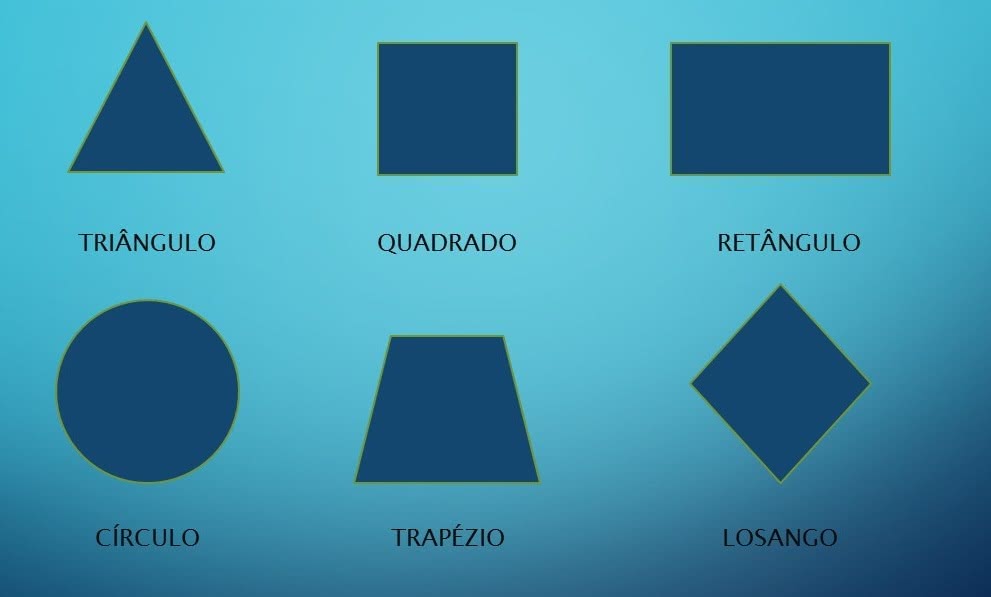
Antes de apresentar as fórmulas das áreas das figuras planas, devemos atentar para cada uma delas:

Triângulo: polígono formado por três lados. São classificados de acordo com as medidas dos lados, bem como seus ângulos:

Quanto a medida dos lados:

• Triângulo Equilátero: apresenta lados e ângulos internos iguais (60°);
• Triângulo Isósceles: apresenta dois lados e dois ângulos internos congruentes;
• Triângulo Escaleno: apresenta todos os lados e ângulos internos diferentes.

Quanto a medida dos ângulos:

• Triângulo Retângulo: possui um ângulo interno de 90°;
• Triângulo Obtusângulo: possui dois ângulos agudos internos, ou seja, menor que 90°, e um ângulo obtuso interno, maior que 90°;
• Triângulo Acutângulo: possui três ângulos internos menores que 90°.

Leia mais sobre triângulo:

• Área do Triângulo
• Perímetro do Triângulo
• Classificação dos Triângulos
• Trigonometria no Triângulo Retângulo

Quadrado: quadrilátero regular formado por quatro lados congruentes (mesma medida). Ele é formado por quatro ângulos internos de 90°, os quais são chamados de ângulos retos.

Leia também:

• Área do Quadrado
• Perímetro do Quadrado

Retângulo: quadrilátero formado por quatro lados, dois deles na vertical e dois na horizontal. Da mesma forma que o quadrado, ele apresenta quatro ângulos internos de 90° (retos).

Leia também:

• Retângulo
• Área do Retângulo
• Perímetro do Retângulo

Círculo: Figura plana também chamada de disco. Apresenta uma forma circular. O raio do círculo representa a medida entre o ponto central da figura e uma das extremidades.

Já o diâmetro equivale duas vezes o raio, posto que representa o segmento de reta que passa pelo centro do círculo, dividindo-o em duas metades iguais.

Leia também:

• Área do Círculo
• Perímetro do Círculo

Trapézio: quadrilátero notável com dois lados e bases paralelas, donde uma é maior e outra menor. A soma de seus ângulos internos totaliza 360°. São classificados em:

• Trapézio Retângulo: apresenta dois ângulos de 90º (ângulos retos);
• Trapézio Isósceles: também chamado de trapézio simétrico donde os lados não paralelos possuem a mesma medida;
• Trapézio Escaleno: todos os lados apresentam medidas diferentes.

Leia também:

• Trapézio
• Área do Trapézio

Losango: quadrilátero equilátero formado por quatro lados iguais. Apresenta dois lados e ângulos opostos congruentes e paralelos, com duas diagonais que se cruzam perpendicularmente. Ele possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).

Saiba mais sobre a Área do Losango.

Fórmula das Áreas das Figuras Planas

Confira abaixo as fórmulas para os cálculos de área:

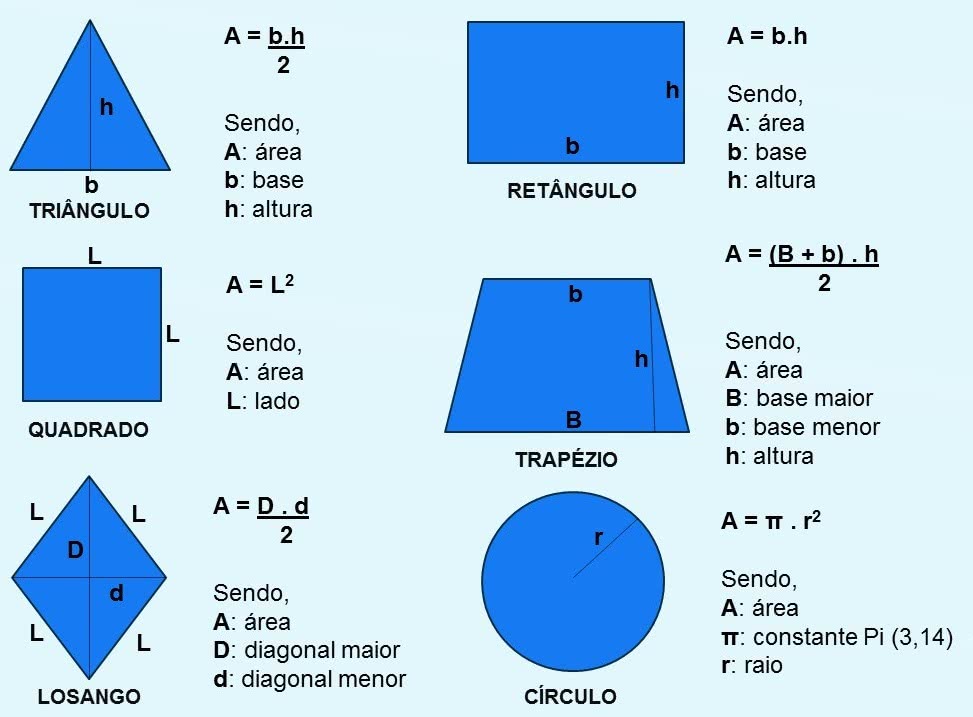
Veja também: Área e Perímetro

Atenção!

Vale lembrar que a área e o perímetro são dois conceitos utilizados na geometria plana, no entanto, apresentam diferenças.

• Área: tamanho da superfície da figura. O valor da área será dado sempre em cm2, m2 ou km2.
• Perímetro: soma de todos os lados da figura. O valor do perímetro será dado sempre em cm, m ou km.

Saiba mais:

• Ângulos
• Área do setor circular
• Quadriláteros
• Perímetros de Figuras Planas
• Polígonos regulares
• Área de Figuras Planas - Exercícios
• Hexágono: definição, área, tipos

Exercícios Resolvidos

Confira abaixo dois exercícios de vestibular sobre áreas de figuras planas.

1. (PUC RIO-2008) Um festival foi realizado num campo de 240 m por 45 m. Sabendo que por cada 2 m² havia, em média, 7 pessoas, quantas pessoas havia no festival?

a) 42.007
b) 41.932
c) 37.800
d) 24.045
e) 10.000

2. (UFSC-2011) Um ciclista costuma dar 30 voltas completas por dia no quarteirão quadrado onde mora, cuja área é de 102400 m². Então, a distância que ele pedala por dia é de:

a) 19200 m
b) 9600 m
c) 38400 m
d) 10240 m
e) 320 m

Confira mais questões, como resolução comentada, em Exercícios sobre Área e Perímetro.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.